As duas únicas forças que agem sobre um corpo têm módulos de e e direções que diferem de . A aceleração resultante tem um módulo de . Qual é a massa do corpo?

Para iniciar essa questão, como trata-se de uma soma vetorial, nada melhor do que começar representando graficamente os vetores, tendo em vista que foi dado o módulo dos vetores e o ângulo entre eles. Para tanto, vamos definir que um dos vetores () esteja paralelo ao eixo que foi definido por nós e o outro () com uma diferença de em relação ao semieixo positivo. Assim:

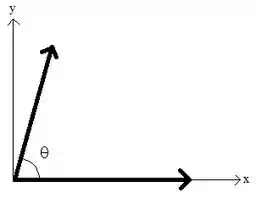
A partir dessa ilustração conseguimos escrever a soma vetorial a partir da combinação das componentes dos vetores, eixo por eixo: