Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 26

Na Fig. 6-23, um trenó é sustentado em um plano inclinado por uma corda que o puxa para cima paralelamente ao plano. O trenó está na iminência de começar a subir. A Fig. 6-28 mostra o módulo F da força aplicada à corda em função do coeficiente de atrito estático μ s entre o trenó e o plano. Se F 1 = 2,0   N , F 2 = 5,0   N e μ 2 = 0,50 , qual é o valor do ângulo θ do plano inclinado?

Passo 1

Vamos iniciar essa questão fazendo uma ilustração do DCL do corpo:

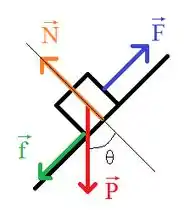
A partir da ilustração acima, podemos aplicar a segunda lei de Newton para cada componente, considerando o equilíbrio em ambos os eixos:

e i x o   x :       F - f - P sin ⁡ θ = 0       e q . 1

e i x o   y :         N - P cos ⁡ θ = 0       e q . 2

Sabendo que f = μ N , então, reescrevendo a e q . 1 :

F - μ N - P sin ⁡ θ = 0       e q . 3

Passo 2

Isolando a normal na e q . 2 :

N = m g cos ⁡ θ

Substituindo na e q . 3 :

F - μ   m g cos ⁡ θ - m g sin ⁡ θ = 0       e q . 4

Passo 3

Com a e q . 4 em mãos, vamos substituir os valores dados no enunciado. Primeiro, para F = 2,0   N e, portanto, μ = 0 :

2 - m g sin ⁡ θ = 0

2 = m g sin ⁡ θ       e q . 5

Isolando m g :

m g = 2 sin ⁡ θ         e q . 6

Agora, vamos fazer de maneira análoga, para F = 5,0   N e μ = 0,5 :

5 - 0,5   m g cos ⁡ θ - m g sin ⁡ θ = 0       e q . 7

Substituindo as equações e q . 5 e e q . 6 na e q . 7 :

5 - 0,5 × 2 sin ⁡ θ × cos ⁡ θ - 2 = 0

tan ⁡ θ = 1 3

Isolando θ :

θ = 18,43 °

Resposta

θ = 18,43 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco A da Fig. 6-33 pesa 102N e o bloco B pesa 32N . Os coeficientes de atrito entre A e a rampa são μ s = 0,56 e μ k = 0,25 . O ângulo θ é igual a 40 ° . Suponha que o eixo x é paralelo à rampa, c
Na Fig. 6-34, os blocos A e B pesam 44N e 22N , respectivamente. (a) Determine o menor peso do bloco C que evita que o bloco A deslize, se μ s entre A e a mesa é 0,20 . (b) O bloco C é removido brusca
Uma caixa de brinquedos e seu conteúdo têm um peso total de 180N . O coeficiente de atrito estático entre a caixa de brinquedos e o piso é 0,42 . A criança da Fig. 6-35 tenta arrastar a caixa puxando-
Na Fig. 6-37, uma prancha de massa m 1 = 40k g repousa em um piso sem atrito e um bloco de massa m 2 = 10k g repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é 0,60
Um pequeno armário com 556N de peso está em repouso. O coeficiente de atrito estático entre o armário e o piso é 0,68 e o coeficiente de atrito cinético é 0,56 . Em quatro diferentes tentativas de des