Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 91
Um pequeno armário com de peso está em repouso. O coeficiente de atrito estático entre o armário e o piso é e o coeficiente de atrito cinético é . Em quatro diferentes tentativas de deslocá-lo, o armário é empurrado por forças horizontais de módulos (a) , (b) , (c) e (d) . Para cada tentativa, calcule o módulo da força de atrito exercida pelo piso sobre o armário. (Em cada tentativa, o armário está inicialmente em repouso.) (e) Em quais das tentativas o armário se move?
Passo 1
Oláaaa, querido! Cê está bem?
Então, temos esse armário:
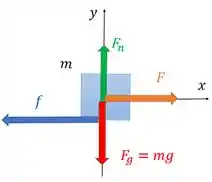
Alguém está aplicando uma força nele para tentar movê-lo. E ele quer saber a força de atrito para cada caso (cada item).
Percebe que no eixo a gente só tem a força de atrito e força aplicada , certo? Então se o armário não se move, quer dizer que a força de atrito é estática e consegue se opor a força , matendo o armário parado. Nesse caso (caso 1), temos
E a necessariamente a força aplicada precisa ser igual ou menor do que a força de atrito estática máxima que o chão consegue fazer nesse cara .
Mas se o ármario se move, significa que a força superou a força de atrito estática, ou seja, . E por isso, a força de atrito é a cinética, dada por
Esse vai ser o nosso caso 2.
Aí precisamos ver se os itens que a gente tem estão no caso 1 ou 2. Ou seja, se neles vamos ter (bloco parado) ou (bloco se movimentando). Bora!
Passo 2
Vamos iniciar essa questão calculando o valor da força de atrito cinético e o valor da força de atrito estático máximo, porque a gente vai precisar delas nos outros itens:
Ih quem é ? Olha no nosso diagrama, na vertical só temos a força peso e a força normal, e não há movimento nessa direção. Então necessariamente força normal e força peso tem o mesmo módulo, assim :
E para a força de atrito máxima, vamos ter:
Com os valores da força de atrito já calculada, vamos comparar as forças para saber em que caso, explicitado no passo anterior, elas se enquadram.
Passo 3
a) Nesse caso, temos . Percebe que esse valor é menor que a força de atrito máximo que vale . Isso quer dizer que a gente está no caso 1, onde o ármario não se move e a força de atrito é
Então,
Passo 4
b) Para , ainda estamos abaixo de , então ainda estamos no caso 1 onde:
Então, o armário também não se move e ;
Passo 5
c) Para , já estamos no caso 2, onde a força aplicada supera o atrito máximo estático de :
Por isso, a nossa força de atrito vai ser a cinética. Logo, o armário se move e ;
Passo 6
d) Para , estamos também no caso 2, onde a força aplicada supera o atrito máximo estático de :
Por isso, a nossa força de atrito vai ser a cinética. Logo, o armário se move e ;
Passo 7
e) o armário se move nos itens c) e d) onde temos o caso 2.
Resposta
- ;
- ;
- ;
- ;
- .