Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 100
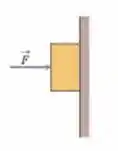
Na Fig. 6-60, um bloco com de peso é mantido em repouso contra uma parede vertical por uma força horizontal de módulo . O coeficiente de atrito estático entre a parede e o bloco é e o coeficiente de atrito cinético é . Em seis experimentos, uma segunda força é aplicada ao bloco, paralelamente à parede, com os seguintes módulos e sentidos: (a) para cima, (b) para cima, (c) para cima, (d) para cima, (e) para baixo e (f) para baixo. Qual é o módulo da força de atrito que age sobre o bloco em cada experimento? Em que experimentos o bloco se move (g) para cima e (h) para baixo? (i) Em que experimentos a força de atrito é para baixo?
Passo 1
Olá, queridão!
Este é um problema bastante extenso, porém o pensamento será repertitivo. Então segura na minha mão e vamos acabar com esse cara!
A ideia aqui é que temos um bloco empurrado contra a parede que está parado. Mas em cada item se aplica uma força vertical, aí queremos avaliar a nova situação do bloco com a atuação de . Vamos começar com o diagrama de corpo livre para a situação nova:
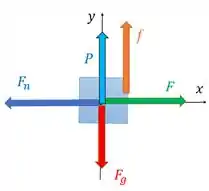
Repara que a gente colocou a força de atrito para cima, mas isso pode mudar dependendo do item. Então essa orientação dela é só para gente ter um referencial positivo. O mesmo vale para a força . Quando ela estiver para baixo, a gente bota um sinal de menos no valor dela, ok?
O que ele quer é saber o valor da força de atrito em cada situação, a orientação dessa força e se o bloco se move. Bem, para que o bloco se mova, a força de atrito encontrada considerando que o corpo está em equilíbrio deve ser maior que a força de atrito estático máximo .
Nesse caso, onde há movimento, o corpo não está de fato em equilíbrio, então a força de atrito dele vai ser na real a cinética .
Caso contrário, o bloco não se move. E por isso a força de atrito é menor ou igual a força de atrito estático máximo, e o seu módulo vai ser o encontrado considerando o equíbrio na vertical .
Temos então 2 casos:
Vamos ver em que caso cada item se encaixa.
Passo 2
Vamos achar a força de atrito estático máxima e a força de atrito cinética, porque a gente vai precisar nos outros itens.
Por isso vamos começar achando o valor da força normal que não muda ao longo dos itens porque é somente vertical. Como no eixo na direção perpendicular a parede não há movimento (), podemos afirmar que:
Com o valor da normal calculada, podemos definir o módulo da força de atrito cinético:
E também o módulo da força de atrito estático máximo:
Passo 3
a) Vamos começar a analisar cada experimento. Primeiro, para (positiva porque atua para cima). Vamos supor que atue para cima, aplicando a segunda lei de Newton considerando o equilíbrio:
Como então nossa suposição de equilíbrio está correta e, portanto, o bloco está em repouso. Além disso, devemos perceber que encontramos um valor negativo de , o que mostra que nossa suposição de sentido está incorreta, e está na verdade para baixo.
Passo 4
b) Para , atuando para cima. Vamos supor novamente que atue para cima. Aplicando a segunda lei de Newton considerando o equilíbrio:
O sinal positivo representa que a força de atrito está no sentido determinado por nós, portanto, a força atua para cima, no mesmo sentido de . Além disso, devemos perceber que e, portanto, o bloco também está em repouso neste experimento.
Passo 5
c) Para , atuando para cima. Supondo qe atue para cima. Aplicando a segunda lei de Newton, considerando o equilíbrio do bloco no eixo paralelo a parede:
Como então nossa suposição de equilíbrio está correta e o bloco está em repouso. E o sinal negativo diz que a força de atrito está para baixo na real.
Passo 6
d) Para , atuando para cima. Continuamos supondo que atue para cima. Aplicando a segunda lei de Newton, considerando o equilíbrio do bloco no eixo paralelo a parede:
Como , então nossa suposição de equilíbrio neste experimento está incorreta e, portanto, .
Esse sinal negativo de para e indica que a força de atrito para baixo não foi suficiente para parar o movimento que tinha a tendencia de fazer subir o bloco. Então o bloco está subindo, e força de atrito cinético está para baixo.
Passo 7
e) Para , atuando para baixo. Supomos agora que atue para cima. Assim, aplicando a segunda lei de Newton e considerando o equilíbrio no eixo paralelo a parede:
Como , então nossa suposição de equilíbrio está correta e o bloco permanece em repouso. E nossa força de atrito está para cima mesmo.
Passo 8
f) Para , atuando para baixo. Supomos novamente que atue para cima. Assim, aplicando a segunda lei de Newton e considerando o equilíbrio no eixo paralelo a parede:
Como , então nossa suposição está incorreta e o bloco está se movendo e .
E como de é positiva, o movimento do bloco se opõe a ela, então ele está para baixo. Daí a gente sabe que a força de atrito real está para cima.
Resposta
- ;
- ;
- ;
- ;
- ;
- .
- ;
- ;
- .