Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.5 - Ex. 16
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são , , e e os ângulos indicados são e . Qual é o trabalho total realizado sobre a caixa pelas três forças nos primeiros de deslocamento?
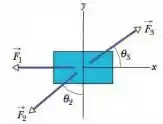
Passo 1
Então galera , como todas as forças são constantes, o trabalho total é dado por , na qual é o módulo da força resultante e é o módulo do deslocamento.
Agora podemos achar as componentes e da força resultante através da relação :
Passo 2
Bom pessoal, agora nós podemos calcular o módulo da força resultante como de costume :
O trabalho realizado pela força resultante , por sua vez , pode ser obtido através da fórmula :
na qual usamos o fato de que (pois a caixa partiu do repouso e se moveu horizontalmente ao ser submetida a forças horizontais, cuja resultante é ) .
Resposta
Tranquilo pessoal?? Bora resolver mais questões então