Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 77
Um ciclista se move em um círculo de de raio com uma velocidade constante de . A massa do conjunto ciclista- bicicleta é . Calcule o módulo (a) da força de atrito que a pista exerce sobre a bicicleta e (b) da força resultante que a pista exerce sobre a bicicleta.
Passo 1
a) Cara, cê tá bem?
Então, ele quer saber a força de atrito que a pista exerce sobre o ciclista em uma curva de .
Cara, quando o ciclista faz a curva, ele tem aceleração centrípeta, que o mantém na rota de trajetória circular. Essa aceleração centrípeta tem essa fórmulinha:
Aí para gerar essa aceleração, é necessário que haja uma força horizontal atuando nele apontando para o centro da trajetória. A única força que pode atuar na horizontal é a força de atrito. Então ela vai ser a força que gera e aponta para o centro da trajetória.
Então, se a gente for fazer um diagrama de corpo livre da situação, vamos ter:
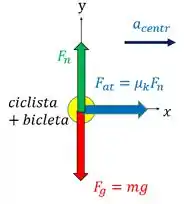
Como fizemos um diagrama de corpo livre, nada mais justo que usar a segunda lei de Newton para resolver essa e achar . Bora lá!
Passo 2
Aplicando a segunda lei de Newton para a direção :
Onde é o conjunto bicleta+ciclista. Nessa direção a gente tem a aceleração centrípeta que vale :
E nessa direção só temos a força de atrito . Substituindo:
Já temos todos esses dados. Então é só substituir e achar :
Passo 3
b) Ele quer a força resultante que a pista exerce sobre o ciclista. As duas forças de superfície que a gente tem são a força normal e a força de atrito . Então a força resultante é a soma dessas duas.
Precisamos achar .
Aplicando a Segunda Lei de Newton à componente vertical do movimento, obtemos , na qual é a força normal exercida pela pista sobre os pneus e é a massa do conjunto ciclista-bicicleta.
Logo:
Passo 4
Bom pessoal, como a força de atrito e a força normal são perpendiculares entre si, para achar o módulo do vetor resultante entre elas duas (que é a força resultante da superfície no ciclista) a gente faz:
Resposta
Tranquilo galera??? Bora resolver mais questões então!!!