Em cada um dos Problemas de 69 a 72, é fornecida uma ou mais equações para resolver um problema. Em cada um deles, você deve
a. Redigir um problema realista para o qual a(s) equação(ções) seja(m) apropriada(s).
b. Desenhar uma representação pictórica correspondente.
c. Resolver o problema proposto.
69.
Passo 1
Opa! Aqui vamos nós de novo!
a) Olha só! Aquele ali na fórmula! Sei não, mas tá cheirando a coeficiente de atrito.
E aquele ali tá cheirando a tração, né não!? De fato, até aqui estamos corretos!
Com isso, acho que já temos dois dados importantes! Dá pra ver que o problema basicamente vai ser um corpo puxado por uma força de tração e o atrito se opondo ao movimento.
Não esquecendo que pela equação, podemos tirar que a massa do corpo é de e sua aceleração é de .
Desse modo! Propomos o seguinte problema...
“Um garoto usa uma corda para puxar uma caixa de , começando da origem, por uma mesa de de comprimento. O coeficiente de atrito cinético entre o livro e a mesa é de . Se a velocidade final do livro é de , qual é a tensão na corda?”
b) E aqui está um esboço pra ajudar melhor na compreensão do problema...
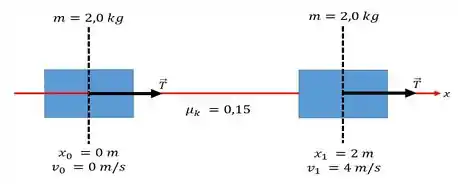
Passo 2
c) Feito o esboço, bora fazer o diagrama de corpo livre para a nossa caixa...
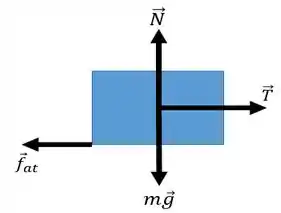
Uma vez que a caixa se move para a direita, a força resultante também apontará para a direita. No caso, a força de tração é no sentido do movimento e a força de atrito se opõe ao movimento.
Com isso, vamos utilizar o Teorema Trabalho e Energia, que diz que a variação de energia cinética é igual ao trabalho da força externa resultante
Substituindo os valores que temos...
Como pode-se ver, chegamos exatamente até a equação proposta! Resolvendo-a...
Obtemos finalmente nossa resposta!
Resposta
a)
“Um garoto usa uma corda para puxar uma caixa de , começando da origem, por uma mesa de de comprimento. O coeficiente de atrito cinético entre o livro e a mesa é de . Se a velocidade final do livro é de , qual é a tensão na corda?”
b)
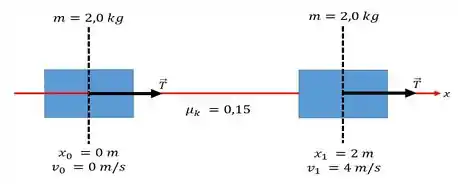
c)