Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.6 - Ex. 41
Uma única força conservativa age sobre uma partícula de que se move ao longo de um eixo . A energia potencial associada a é dada por
onde está em metros. Em , a partícula possui uma energia cinética de . (a) Qual é a energia mecânica do sistema? (b) Faça um gráfico de em função de x para e plote, no mesmo gráfico, a reta que representa a energia mecânica do sistema. Use o gráfico do item (b) para determinar (c) o menor valor de que a partícula pode atingir e (d) o maior valor de que a partícula pode atingir. Use o gráfico do item (b) para determinar (e) a energia cinética máxima da partícula e (f) o valor de para o qual a energia cinética atinge este valor. (g) Escreva uma expressão para , em newtons, em função de , em metros. (h) para que valor (finito) de ?
Passo 1
a) e em
E , logo
Passo 2
b) O gráfico é mostrado na figura abaixo
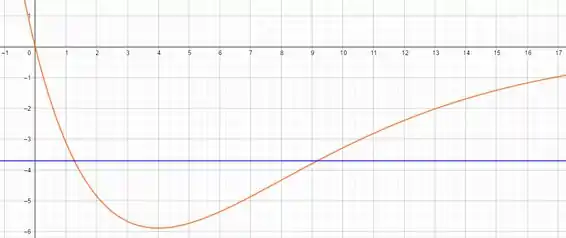
Passo 3
c) Os pontos procurados são onde a energia mecânica é igual a energia potencial. Logo, pelas interseções no gráfico, pode-se encontrar esses valores. Para o menor valor
Passo 4
d) Para o maior valor
Passo 5
e) O menor valor de será quando a energia cinética é máxima em , é mínimo e vale
A energia cinética será
Passo 6
f) Como visto no item e)
Passo 7
g) será dado por
Passo 8
h) Para
Resposta
a)
b)
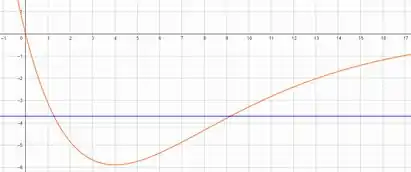
c)
d)
e)
f)
g)
h)