Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.Problemas - Ex. 81

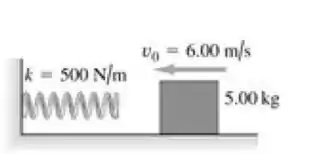
Um bloco de 5,0 kg se move com v0 = 6,0 m/s sobre uma superfície horizontal sem atrito, dirigindo-se contra uma mola cuja constante é dada por k = 500 N/m e que possui uma de suas extremidades presa a uma parede. A massa da mola é desprezível.

a) Calcule a distância máxima que a mola pode ser comprimida.

b) Se a distância máxima que a mola pudesse ser comprimida fosse de 0,150 m, qual seria o valor máximo de vo?

Passo 1

Como o problema trata de um corpo em movimento juntamente com um sistema mola, temos dois tipos de energia atuando: a energia cinética e a energia elástica. Então temos:

E c = m v 2 2 e E l = k x 2 2

Igualando as duas equações já que ambas tratam de energia:

k x 2 2 =   m v 2 2

Agora basta substituir os valores e encontrar o valo de v! Essa foi bem fácil né?

Passo 2

Calculando...

k x 2 2 =   m v 2 2

500 x 2 2 =   5 ( 6 2 ) 2

x 2 = 0,36

x = 0,6   m

Passo 3

Façamos o mesmo calculo da questão anterior, porém dessa vez foi fornecido o valor de X e pedido a velocidade, logo:

k x 2 2 =   m v 2 2

Isolando a velocidade, teremos:

v = k m x

Ué? Essa conseguiu ser mais fácil que a primeira! Então vamos responder.

Passo 4

Substituindo os valores...

v = k m x

v = 500 5 0,15

v = 1,5   m / s

Resposta

Resposta: (a) A distância é igual a 0,6 metros.

Resposta: (b) A velocidade máxima é igual a 1,5 m/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

133- Uma força conservativa F ( x ) age sobre uma partícula que se move ao longo de um eixo x. A Fig. 8- 72 mostra a variação da energia potencial U ( x ) associada a F ( x ) com a posição da partícul
135- Repita o Problema 83 supondo que o bloco está subindo uma rampa que faz um ângulo de 5,0° com a horizontal.
No Problema 2, qual é a velocidade do carro (a) no ponto A , (b) no ponto B e (c) no ponto C ? (d) Que altura o carro alcança na última elevação, que é alta demais para ser transposta? (e) Se o carro
67. Nos problemas de 64 a 67 , são fornecidas equações para serem usadas na resolução de um problema. Para cada uma delas, você deve Redigir um problema realista para o qual esta equação se aplique. D
60. A molécula N H 3 de amônia tem a estrutura tetraédrica mostrada na FIGURA P10.60a. Os três átomos de hidrogênio formam um triângulo no plano x y em z = 0 . O átomo de nitrogênio constitui o vértic