Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.6 - Ex. 40

A Fig. 8-47 mostra um gráfico da energia potencial U em função da posição x   para urna partícula de 0,200   k g que pode se deslocar apenas ao longo de um eixo x sob a influência de uma força conservativa. Três dos valores mostrados no gráfico são U A   =   9,00   J , U c   =   20,00   J e U D   =   24,00   J . A partícula é liberada no ponto onde U forma uma "barreira de potencial" de "altura" U B   =   12,00   J , com uma energia cinética de 4,00   J . Qual é a velocidade da partícula (a) em x   =   3,5   m e (b) em x   =   6,5   m ? Qual é a posição do ponto de retorno (c) do lado direito e (d) do lado esquerdo?

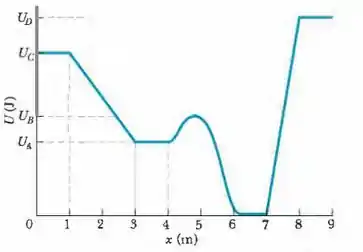
Figura 8-47 Problema 38

Passo 1

a) Pela lei da conservação da energia

K A + U A = K B + U B

Para U A = 9   J , K B = 4   J e U B = 12   J

K A + 9 = 4 + 12

K A = 7

m v 2 2 = 7

v = 14 m

Para m = 0,2   k g

v = 14 0,2

v = 8,37   m / s

Passo 2

b) Em x = 6,5   m , U = 0 . Pela lei da conservação da energia

K + U = K B + U B

K = 12 + 4

K = 16   J

Logo

v = 2.16 0,2

v = 12,6   m / s

Passo 3

c) No ponto de retorno a velocidade da partícula é zero. Fazendo interpolação entre x = 7   m , x = 8   m , teremos

7   m         -           0

x   m   -     16   J

8   m         -             24   J

x - 7 8 - 7 = 16 - 0 24 - 0

x = 7,67   m

Passo 4

d) Usando interpolação entre x = 3   m , x = 1   m

3   m         -           9

x   m   -     16   J

1   m         -             20   J

x - 3 1 - 3 = 16 - 9 20 - 9

x = 1,73   m

Resposta

a) v = 8,37   m / s

b) v = 12,6   m / s

c) x = 7,67   m

d) x = 1,73   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto se desloca no plano xy submetido à ação de uma força conservativa descrita pela função energia potencial dada por U x ,y = α ( 1 x 2 + 1 y 2 ) , onde α é uma constante positiva.Deduza uma ex
Duas massas, m 1 e m 2 , estão sobre o eixo x, sendo m1 mantido no lugar de origem e m 2 naposição x, livre para se mover. A energia potencial gravitacional dessas massas é dada por U x = - G m 1 m 2
Uma força paralela ao eixo Ox atua sobre uma partícula que se desloca ao longo deste eixo. Essa força produz uma energia potencial dada por U x = α x 4 , onde α = 1,20J / m 4 . Qual é aforça (módulo,
A energia potencial entre dois átomos de hidrogênio separados por uma distância x muito grande é dada por U x = - C 6 / x 6 , onde C 6 é uma constante positiva. Qual é a força que um átomo exerce sobr
Duas massas, m 1 e m 2 , estão sobre o eixo xy, estando m 1 posicionado no lugar de origem e m 2 , na posição x e livre para mover-se por uma distância r de um ponto P com coordenadas x e y (Figura 7.