Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.6 - Ex. 39
A Fig. 8-48 mostra um gráfico da energia potencial em função da posição para uma partícula de que pode se deslocar apenas ao longo de um eixo . (Forças dissipativas não estão envolvidas.) Os três valores mostrados no gráfico são , e . A partícula é liberada em com uma velocidade inicial de , no sentido negativo de . (a) Se a partícula puder chegar ao ponto , qual será sua velocidade nesse ponto? Se não puder, qual será o ponto de retomo? Quais são (b) o módulo e (c) a orientação da força experimentada pela partícula quando ela começa a se mover para a esquerda do ponto ? Suponha que a partícula seja liberada no mesmo ponto e com a mesma velocidade, mas o sentido da velocidade seja o sentido positivo de . (d) Se a partícula puder chegar ao ponto , qual será sua velocidade nesse ponto? Se não puder, qual será o ponto de retorno? Quais são (e) o módulo e (f) a orientação da força experimentada pela partícula quando ela começa a se mover para a direita do ponto ?
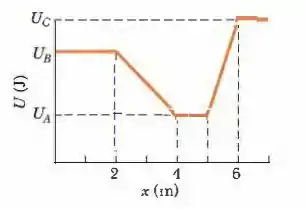
Figura 8-48 Problema 39.
Passo 1
- Oi, pessoal! Tudo bom? Nessa questão vamos aplicar a conservação da energia!
Vamos analisar o momento inicial , onde , e .
Repara que temos que calcular . Para e
Logo a energia mecânica será:
Como a energia mecânica é maior do que a energia potencial no ponto (, a partícula consegue chegar nesse ponto.
Em , . Logo pela lei da conservação da energia
Agora que achamos a energia cinética de , podemos encontrar a velocidade,
Isolando ,
Portanto a velocidade da partícula em é de .
Passo 2
b) A força é dada por
E como o gráfico é o de uma reta, temos que a derivada é dada por:
Usando os pontos e
Passo 3
c) Como , a força é no sentido positivo de
Passo 4
d) Em , , maior que a energia mecânica e a partícula não consegue chegar nesse ponto.
Logo, temos um ponto de retorno onde , esse ponto irá acontecer quando a energia potencial for igual a energia mecânica .
Por interpolação entre os pontos e :
Portanto, o ponto de retorno será em .
Passo 5
e) A força é dada por
E por ser uma reta a derivada é dada como:
Usando os pontos e
E o seu módulo é
Passo 6
f) Como , a força é no sentido negativo de
Resposta
a)
b)
c) sentido positivo de
d)
e)
f) sentido negativo de