Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.2 - Ex. 6

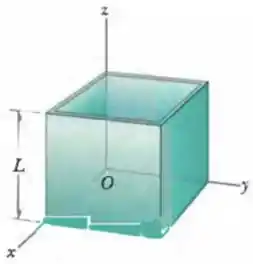
A Fig. 9-39 mostra uma caixa cúbica que foi construída com placas metálicas uniformes de espessura desprezível. A caixa não tem tampa e tem uma aresta L = 40   c m . Determine (a) a coordenada x , (b) a coordenada y e (c) a coordenada z do centro de massa da caixa.

Passo 1

Oi, galerinha! Tudo bom? Aqui nós temos que calcular o centro de massa de uma figura em 3 D , onde cada face tem uma massa. Repara que a caixa não tem tampa, sendo um total de 5 faces. Além disso, temos uma caixa cúbica homogênea, todas as faces possuem a mesma massa. Deste modo, vamos aplicar:

x c m = m x 1 + m x 2 + m x 3 + m x 4 + m x 5 5 m

y c m = m y 1 + m y 2 + m y 3 + m y 4 + m y 5 5 m

z c m = m z 1 + m z 2 + m z 3 + m z 4 + m z 5 5 m

Onde, m i é a massa de cada partícula, x i é a posição do centro de massa no eixo x , y i é a posição do centro de massa no eixo y e z i é a posição do centro de massa no eixo z .

Passo 2

Vamos iniciar escrevendo as coordenadas das cinco faces:

f a c e   n o   p l a n o   y z :   x 1 , y 1 , z 1 = 0,20,20

f a c e   n o   p l a n o   x z : x 2 , y 2 , z 2 = ( 20,0 , 20 )

f a c e   n o   p l a n o   x y : x 3 , y 3 z 3 = ( 20,20,0 )

f a c e   p a r a l e l a   a o   p l a n o     y z : x 4 , y 4 , z 4 = 40,20,20

f a c e   p a r a l e l a   a o   p l a n o   x z : x 5 , y 5 , z 5 = 20,40,20

Passo 3

  1. Portanto, a coordenada x do centro de massa é:

    2. x c m = m 0 + 20 m + 20 m + 40 m + 20 m 5 m = 20   c m

    Repara que esse m é de massa e podemos coloca-lo em evidencia:

    x c m = m 20 + 20 + 40 + 20 5 m

    x c m = 20 + 20 + 40 + 20 5 = 20   c m

    Agora vamos aplicar o mesmo raciocínio para as outras coordenadas.

    Passo 4

  2. A coordenada y do centro de massa:

    3. y c m = 20 m + m 0 + 20 m + 20 m + 40 m 5 m = 20   c m

    Passo 5

  3. Por fim, a coordenada z do centro de massa:

z c m = 20 m + 20 m + 0 m + 20 m + 20 m 5 m = 16   c m

Resposta

  1. x c m = 20   c m ;
  2. y c m = 20   c m ;
  3. z c m = 16   c m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma lata em forma de cilindro simétrico de massa M e altura H está cheia de água. A massa inicial da água é M , mesma massa da lata. Um pequeno buraco é feito no fundo da lata, e a água começa a escor
Encontre o centro de massa da folha uniforme de madeira na figura. Considere esse sistema como efetivamente composto de duas folhas, supondo que uma “massa negativa” para compensar o buraco. Portanto,
Repita a análise do problema 107 com um ângulo geral θ na junção, ao invés de 90 ° . Sua resposta concorda com o resultado específico para o problema 90 ° ? A sua resposta dá resultados plausíveis par
Mostre que o centro de massa de um disco semicircular de raio R está sobre um ponto a 4 R / 3 π do centro do círculo.
Você lança um bumerangue, por um tempo, ele "voa" horizontalmente em linha reta com rapidez constante, ao mesmo tempo que girando rapidamente em torno de si próprio. Desenhe uma série de figuras, com