Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 108

Repita a análise do problema 107 com um ângulo geral θ na junção, ao invés de 90 ° . Sua resposta concorda com o resultado específico para o problema 90 ° ? A sua resposta dá resultados plausíveis para os ângulos 0 ° e 180 ° ?

Passo 1

Vamos começar fazendo um esquema da situação:

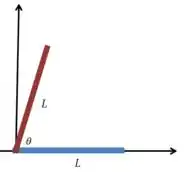
Vamos definir um sistema de coordenadas em que o eixo x está sempre sobre uma das hastes, e θ é o ângulo entre as duas hastes. Quais são as coordenadas do centro de massa de cada uma:

C 1 :           L 2 cos ⁡ θ   , L 2 sen ⁡ θ

C 2 :         L 2 ,   0

Passo 2

Agora vamos calcular as coordenadas do centro de massa em cada eixo, considerando que a massa de cada haste é m :

x C M = L 2 cos ⁡ θ m + L 2 m 2 m = L 4 cos ⁡ θ + 1

y C M = 0 m + L 2 sen ⁡ θ ( m ) 2 m = L 4 sen ⁡ θ

Passo 3

Beleza, já encontramos as fórmulas que procurávamos, agora vamos analisar os ângulos que foram pedidos.

No caso em que θ = 90 ° :

x C M = L 4 cos ⁡ 90 ° + 1 = L 4

y C M = L 4 sen ⁡ 90 ° = L 4

O que concorda com a resposta anterior.

No caso em que θ = 0 ° :

x C M = L 4 cos ⁡ 0 ° + 1 = L 2

y C M = L 4 sen ⁡ 0 ° = 0

Isso faz sentido, já que nesse caso as duas hastes estão sobrepostas, e totalmente localizadas no eixo x , é natural que o centro de massa esteja no ponto médio comum das duas.

No caso em que θ = 180 ° :

x C M = L 4 cos ⁡ 18 0 ° + 1 = 0

y C M = L 4 sen ⁡ 18 0 ° = 0

Isso também faz sentido, já que nesse caso ambas as hastes estão no eixo x , mas uma está sobre a porção negativa e a outra sobre a positiva. É natural que o centro de massa esteja na origem, já que o sistema é simétrico em relação ao eixo y .

Resposta

A resposta concorda com o resultado anterior, e dá resultados plausíveis para os ângulos θ = 0 ° e θ = 180 ° .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas partículas de 3,0k g têm velocidades v → 1 = 2,0 m s i ^ + 3,0 m s j ^ e v → 2 = 4,0 m s i ^ - 6,0 m s j ^ . Encontre a velocidade do centro de massa do sistema.
Uma força F → = 12Ni ^ é aplicada à bola de 3,0k g na figura do problema 103 . (Nenhuma força age nas outras duas bolas). Qual é a aceleração do centro de massa do sistema de três bolas?Figura do prob
Encontre a localização do centro de massa de uma barra não-uniforme de 0,40m de comprimento se a sua densidade varia linearmente de 1,00g / c m em uma ponta até 5,00g / c m na outra ponta. Especifique
Na máquina de Atwood abaixo a corda passa por cima do cilindro fixo de massa m C . O cilindro não roda. Ao invés disso, a corda desliza sobre a sua superfície sem atrito. (a) Encontre a aceleração do
Você tem um arame uniforme e fino dobrado em um arco circular, que é descrito por um raio R e um ângulo θ m (veja a figura). Mostre que a localização do centro de massa do é sobre o eixo x , a uma dis