Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 109
Mostre que o centro de massa de um disco semicircular de raio está sobre um ponto a do centro do círculo.
Passo 1
Falaa! Ele quer que a gente localize o centro de massa de um disco semicircular. Nesse caso vamos precisar usar o cálculo integral porque queremos fazer uma demonstração.
Como estamos lidando com um disco semicircular, é uma boa ideia usar coordenadas polares. Ao usar essas coordenadas, precisamos pensar que nossas variáveis nele são (tamanho de um segmento que sai da origem) e (orientação desse segmento).
E que elas se relacionam com e assim:
Vamos esboçar nosso disco e nosso referencial:
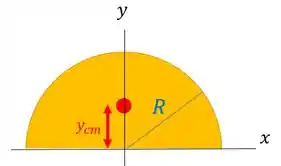
Com a origem localizada no centro do disco, o sistema fica simétrico em torno do eixo , por isso uma das coordenadas do centro de massa é:
E fica faltando determinar a outra. Ou seja, vamos usar integrais para achar .
Passo 2
A expressão para achar o centro de massa de objetos delgados (barras e arcos) é essa
Mas como temos uma superfície plana (um disco), essa integral vai ser dupla:
Onde e . Só que como já sabemos , só precisamos calcular essa expressão para a componente . Ou seja, queremos:
A ideia é montar essa integral.
Vamos considerar uma pequena área do disco, que a gente chama de elemento infinitesimal de área. Em coordenadas polares, a área de um elemento infinitesimal tem essa expressão:
Só que queremos a massa desse elemento. Vamos escrever essa bonita considerando que o disco tem densidade supercial uniforme . A gente escreve densidade superficial dividindo massa por área. Então para o nossos elemento infinitesimal vamos ter
Isolando o que a gente quer:
E sabendo que :
Substituindo isso na nossa expressão de e lembrando que :
Passo 3
Temos:
Precisamos dos intervalos de e onde temos o nosso disco:
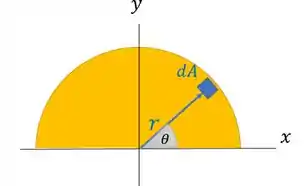
é o tamanho do segmento que sai da origem. Então ele começa em (a própria origem). E o valor máximo dele é o próprio raio do disco . Assim:
Já é o ângulo que faz com . Como temos apenas a parte de cima do círculo, vamos ter:
Posicionando esses extremos de acordo com cada variável:
Percebe que a integral de fora está em relação a , aí ela vai ter nos extremos o intervalo de . E a integral de dentro fica com os extremos de .
Passo 4
Agora é calcular.
Primeiro a integral de dentro. A gente pode tirar de dentro dela tudo que está em produto com uma função de e não é uma função de (é constante em relação a ):
A integral indefinida de é , então:
E podemos tirar dessa integral tudo que está em produto com a função de e não é função de :
E a integral indefinida do é , substituindo os limites de integração ficamos com:
Passo 5
Agora vamos montar uma expressão para . Essa é a densidade superficial do disco. A densidade superficial é dada pela razão entre massa e área do objeto:
E a área do semicírculo é metade da área do círculo:
Então:
Substituindo no resultado de antes:
E essa é a distância do centro de massa até a origem.
Resposta
Demonstração.