Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.3 - Ex. 13

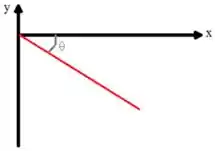
A Fig. 9-44 mostra um arranjo com um trilho de ar no qual um carrinho está preso por uma corda a um bloco pendurado. O carrinho tem massa m 1 = 0,600   k g e o centro do carrinho está inicialmente nas coordenadas x y ( - 0,500   m ,   0   m ) ; o bloco tem massa m 2 = 0,400   k g e o centro do bloco está inicialmente nas coordenadas x y   ( 0 ,   - 0,100   m ) . As massas da corda e da polia são desprezíveis. O carrinho é liberado a partir do repouso e o carrinho e o bloco se movem até que o carrinho atinja a polia. O atrito entre o carrinho e o trilho de ar e o atrito da polia são desprezíveis. (a) Qual é a aceleração do centro de massa do sistema carrinho-bloco em termos dos vetores unitários? (b) Qual é o vetor velocidade do CM em função do tempo t ? (c) Plote a trajetória do CM. (d) Se a trajetória for curva, verifique se apresenta um desvio para cima e para a direita ou para baixo e para a esquerda em relação a uma linha reta; se for retilínea, calcule o ângulo da trajetória com o eixo x .

Passo 1

Devemos perceber que a força resultante, considerando o sistema formado pelos dois blocos será:

F R → = - m 2 g j ^

Pois as trações são forças internas, e o peso do primeiro bloco se cancela com a normal. Assim, aplicando a segunda lei de Newton para este sistema, temos:

F R = m 1 + m 2 a

Isolando a :

a = F R m 1 + m 2 = m 2 g m 1 + m 2

Substituindo os valores:

a = 0,4 × 9,8 0,6 + 0,4 = 3,92   m / s 2

Passo 2

Com o valor da aceleração em mãos, devemos perceber que o primeiro bloco está acelerado com esta aceleração para direita ( a → 1 = 3,92 i ^   m / s 2 ) e o segundo bloco está acelerado com esta mesma aceleração para baixo ( a → 2 = - 3,92 j ^   m / s 2 ). Portanto, podemos agora aplicar a seguinte relação para determinar a aceleração do centro de massa:

a → C M = m 1 a → 1 + m 2 a → 2 m 1 + m 2

Substituindo os valores:

a → C M = 0,6 × 3,92 i ^ + 0,4 × - 3,92 j ^ 0,6 + 0,4

a → C M = 2,35 i ^ - 1,57 j ^   m / s 2

Passo 3

Para determinar o   v → ( t ) , devemos integrar o a → C M :

v → t = ∫ 0 t a → t   d t

v → = 2,35 i ^ - 1,57 j ^ t + v 0 →

Como o sistema parte do repouso, então:

v → t = 2,35 i ^ - 1,57 j ^ t   m / s

Passo 4

Devemos perceber que:

tan ⁡ θ = v y v x

É constante durante todo o movimento. Substituindo os valores:

tan ⁡ θ = - 1,57 t 2,35 t

Isolando θ :

θ = tan - 1 ⁡ - 1,57 2,35 = - 33,7 °

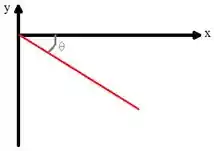
Como este valor é constante em todo o movimento, então o centro de massa descreve uma trajetória retilínea cuja a reta faz um ângulo, para baixo, de 34 ° com a horizontal.

Passo 5

Como o gráfico da posição do centro de massa é uma reta que faz um ângulo de 34 ° com a horizontal, considerando que inicialmente, a posição do centro de massa é nula, temos:

Resposta

  1. a → C M = 2,35 i ^ - 1,57 j ^   m / s 2 ;
  2. v → t = 2,35 i ^ - 1,57 j ^ t   m / s ;
  4. R e t i l í n e o   c o m   θ = 34 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 9-43, duas partículas são lançadas da origm do sistema de coordenadas no instante t = 0 . A partícula 1 , de massa m 1 = 5,00g , é lançada horizontalmente para a direita, em um piso sem atrito
Um canhão dispara um projétil com uma velocidade inicial v 0 = 20m / s e um ângulo θ 0 = 60 ° com a horizontal. No ponto mais alto da trajetória, o projétil explode em dois fragmentos de massas iguais
Uma bola de softball de 0,30k g tem uma velocidade escalar de 15m / s e um ângulo de 35 ° abaixo da horizontal imediatamente antes de ser golpeada por um taco. Qual é o módulo da variação do momento l
No instante t = 0 , uma bola é lançada para cima a partir do nível do solo, em terreno plano. A Fig. 9-46 mostra o módulo p do momento linear da bola em função do tempo t após o lançamento ( p 0 = 6,0