Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.5 - Ex. 22

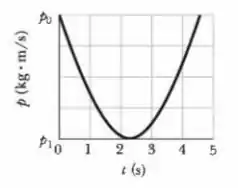
No instante , uma bola é lançada para cima a partir do nível do solo, em terreno plano. A Fig. 9-46 mostra o módulo do momento linear da bola em função do tempo após o lançamento ( e ). Determine o ângulo de lançamento. (Sugestão: procure uma solução que não envolva a leitura no gráfico do instante em que passa pelo valor mínimo.)

Passo 1

Podemos resolver esta questão tirando aquele coelho mágico da cartola. Para tanto, devemos perceber que o momento mínimo significa o instante em que a bola atinge a altura máxima e, portanto, . Assim, a componente horizontal é igual ao momento total:

Passo 2

Como a componente horizontal é constante e módulo do momento inicial, de acordo com o gráfico, é , então, escrevendo a componente horizontal do momento, temos:

Como já calculamos e foi extraído no gráfico, então:

Isolando :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mina explode em três fragmentos, de 100g cada um, que se deslocam num plano horizontal: um deles para oeste e os outros dois em direções 60 ° ao norte e 30 ° ao sul da direção leste, respectivamen

João e José estão sentados em um trenó que está inicialmente em repouso sobre uma superfície de gelo sem atrito. O peso de João é igual a 800N , o peso de José é igual a 600N e o peso do trenó é igual

Durante uma missão lunar é necessário aumentar a velocidade de uma espaçonave em 2,2m / s quando ela está se movendo a 400m / s em relação à Lua. A velocidade dos produtos de exaustão do motor do fogu

Uma bola de 0,550k g cai verticalmente sobre um piso de concreto, atingindo-o com uma velocidade escalar de 12,0m / s e ricocheteando verticalmente para cima com uma velocidade escalar de 3,00m / s .

Um pacote de 2,65k g , inicialmente em repouso, explode em três partes que deslizam em um piso sem atrito. O pacote estava inicialmente na origem de um sistema de coordenadas. A parte 1 tem massa m 1