Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Exercício - Ex. 23

Suponha que o capacitor de 3   μ F , na figura 24.10a, seja removido e substituído por outro, alterando a capacitância equivalente entre os pontos a e b para 8   μ F . Qual é o valor da capacitância do capacitor que substitui o primeiro?

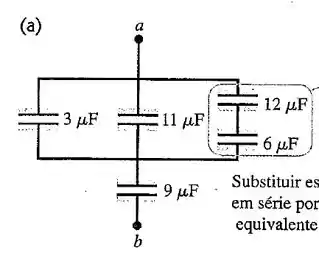
Passo 1

Para associação de capacitores:

i ) C a p a c i t o r e s   e m   p a r a l e l o :

C e q = C 1 + C 2 + . . .

Q = Q 1 + Q 2 + . . .

V 1 = V 2 = V

i i ) C a p a c i t o r e s   e m   s é r i e :

1 C e q = 1 C 1 + 1 C 2 + . . .

Q 1 = Q 2 = Q

V = V 1 + V 2 + . . .

Passo 2

Vamos chamar:

C 1 = 3 ⋅ 10 - 6     F

C 2 = 11 ⋅ 10 - 6     F

C 3 = 12 ⋅ 10 - 6     F

C 4 = 6 ⋅ 10 - 6     F

C 5 = 9 ⋅ 10 - 6     F

Passo 3

Vamos substituir C 1 por outro capacitor que vamos chamar de C ' 1 .

Queremos saber quem é C ' 1 sabendo que agora C e q = 8 ⋅ 10 - 6   F .

Passo 4

Agora os capacitores C 3 e C 4 estão em série. Logo:

1 C 34 = 1 C 3 + 1 C 4

1 C 34 = 1 12 ⋅ 10 - 6 + 1 6 ⋅ 10 - 6

1 C 34 = 1 + 2 12 ⋅ 10 - 6

1 C 34 = 3 12 ⋅ 10 - 6

C 34 = 4 ⋅ 10 - 6   F

Passo 5

Os capacitores C ' 1 , C 2 e C 34 estão em paralelo logo:

C 1 ' 234 = C ' 1 + C 2 + C 34

C 1 ' 234 = C ' 1 + 11 ⋅ 10 - 6 + 4 ⋅ 10 - 6

C 1 ' 234 = C ' 1 + 15 ⋅ 10 - 6

Passo 6

Agora, C 1 ' 234 e C 5 estão em série:

1 C e q = 1 C 1 ' 234 + 1 C 5

Substituindo os valores:

1 8 ⋅ 10 - 6 = 1 C 1 ' 234 + 1 9 ⋅ 10 - 6  

1 8 ⋅ 10 - 6 - 1 9 ⋅ 10 - 6   = 1 C 1 ' 234

1 C 1 ' 234 = 9 - 8 72 ⋅ 10 - 6

C 1 ' 234 = 72 ⋅ 10 - 6   F

Passo 7

Como já achamos a expressão para C 1 ' 234 , só precisamos substituir.

C ' 1 + 15 ⋅ 10 - 6 = 72 ⋅ 10 - 6  

C ' 1 = 57 ⋅ 10 - 6   F

Resposta

C ' 1 = 57 ⋅ 10 - 6   F

letra b) Q = 173,5 ⋅ 10 - 6   C

letra c) Q 1 = 173,5 ⋅ 10 - 6   C , Q 4 = 173,5 ⋅ 10 - 6   C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quantos capacitores de 1,00μ F conectados em paralelo seriam necessários para armazenar uma carga total de 1,00m C se a diferença de potencial em cada capacitor fosse 10,0V ? Faça um diagrama da combi
Para o circuito mostrado na Figura 24-37 determine A capacitância equivalente entre os terminais.A carga armazenada na placa carregada positivamente de cada capacitor.A tensão em cada capacitor, e;A e
Mostre que a capacitância equivalente para dois capacitores em série pode ser escrita como C e q = C 1 C 2 C 1 + C 2 Usando apenas esta formula e um pouco de álgebra, mostre que C e q deve ser, sempre
Para o circuito mostrado na Figura 24-36...Os capacitores foram todos descarregados antes de serem conectados à fonte de tensão. Determine (a) a capacitância equivalente da combinação(b) a carga armaz
Determine as diferentes capacitâncias equivalentes que podem ser obtidas usando dois ou três dos seguintes capacitores: um capacitor de 1,00μ F , um capacitor de 2,00µ F µ e um capacitor de 4,00µ F µ