Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 5.Problemas - Ex. 5

Ache a capacitância equivalente ao sistema da figura, entre os pontos a e b .

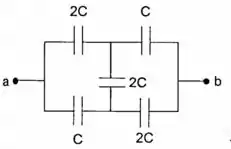
Passo 1

Para facilitar nosso trabalho, podemos numerar os capacitores, como na figura, para melhorar a identificação. Beleza?!

Levando em consideração que o conjunto dos capacitores ( C 1 , C 4   ) e ( C 2 , C 5   ) estão em paralelo, podemos dizer que o potencial é constante. Isso resulta em

V a - V b = V 2 + V 5                           ( 1 )

V a - V b = V 1 + V 4                           ( 2 )

V a - V b = V 1 - V 3 + V 5       3

Passo 2

Agora, se separarmos os conjuntos como na imagem a seguir temos que encontrar que a soma das cargas deve ser zero.

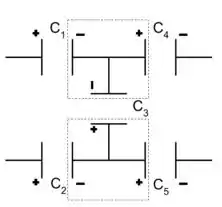
Daí temos

- Q 1 + Q 4 - Q 3 = 0 - Q 2 + Q 5 + Q 3 = 0

Lembrando que Q = C V e substituindo os valores das capacitâncias, temos

- 2 C V 1 + C V 4 - 2 C V 3 = 0 - C V 2 + 2 C V 5 + 2 C V 3 = 0 ⇒ - 2 V 1 + V 4 - 2 V 3 = 0           ( 4 ) - V 2 + 2 V 5 + 2 V 3 = 0         ( 5 )

Passo 3

Levando em consideração que a carga nos capacitores do lado esquerdo deve ser igual à do lado direito, temos

Q T = Q 1 + Q 2 = Q 4 + Q 5 ⇒ C e q V = C 1 V 1 + C 2 V 2

Passo 4

Agora precisamos manipular as equações para obter uma relação entre a ddp entre os terminais a e b com a ddp entre os capacitores individuais

Da equação (5) podemos escrever

2 V 3 = V 2 - 2 V 5

Substituindo nas equações (4) e (3)

- 2 V 1 + V 4 - V 2 + 2 V 5 = 0       ( 6 )

                V 1 - V 2 2 + 2 V 5 = V                               7          

Da equação (2), temos

V 4 = V - V 1

Aplicando isto na eq (6)

- 3 V 1 + 3 V - 3 V 2 = 0 ⇒ - V 1 + V - V 2 = 0       ( 8 )

Usando a equação (1), temos

V 5 = V - V 2

Substituindo em (7)

V 1 - V 2 2 + 2 V - 2 V 2 = V     ( 9 )

Substituindo na eq (8), temos

- V 1 + 3 V - V 2 = 0       ( 10 )

Arrumando as equações (9) e (10)

V 1 - 5 2 V 2 = V

V 1 + V 2 = V

Através das últimas duas equações podemos relacionar V 1 , V 2 , V 3 , V 4 e V 5 com V

V 1 = 3 7 V ;   V 2 = 4 7 V ; V 3 = - 1 7 V ; V 4 = 4 7 V ; V 5 = 3 7 V

Passo 5

Agora vamos retornar para a equação da carga total

C e q V = C 1 V 1 + C 2 V 2

Substituindo os valores, teremos

C e q = 6 7 C + 4 7 C = 10 7 C

Resposta

C e q = 10 7 C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura 24-46 mostra quatro capacitores conectados no arranjo conhecido como uma capacitância em ponte. Os capacitores estão inicialmente descarregados. Qual deve ser a relação entre as quatro capaci
Determine a capacitância equivalente, em termos de C 0 de cada uma das combinações de capacitores mostrada na Figura 24-25.
Dois capacitores idênticos, descarregados, estão conectados em série aos terminais de uma bateria de 100V . Quando apenas um dos capacitores está conectado nos terminais da bateria, a energia armazena
Cinco capacitores idênticos com capacitância C 0 estão conectados em uma rede em ponte, como mostrado na Figura 24 - 38 .Qual é a capacitância equivalente entre os pontos a e b ?Determine a capacitânc
Um capacitor de 10,0µ F µ e um capacitor de 20,0μ F estão conectados em paralelo aos terminais de uma bateria de 6,00V .(a) Qual é a capacitância equivalente desta combinação?(b) Qual é a diferença de