Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.9 - Ex. 31
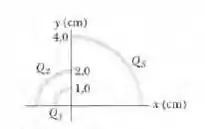
Na Fig. abaixo, três barras finas de plástico têm a forma de quadrantes de circunferência com o mesmo centro de curvatura, situado na origem. As cargas uniformes das barras são = +30 nC, = +3,0 e = - 8,0. Determine o potencial elétrico na origem.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Essa questão explora uma característica do potencial elétrico. Lembre-se que ele é escalar. Mas você deve estar me perguntando, o que isso tem a ver com a questão? Bem, diferente do campo elétrico, que em questões desse tipo a gente tinha que calcular o vetor campo elétrico, agora nós podemos nos concentrar apenas na distância que esses arcos estão do ponto em que estamos calculando o potencial, que é a origem.
Passo 2
Uma característica desse tipo de questão é que essas barras podem ser substituídas por cargas pontuais. Isso foi melhor explicado no exercício 24 desse capítulo.
Lá descobrimos que o potencial elétrico no centro desses arcos é dado por:
Em que R é o raio e é a permissividade do vácuo.
Substituindo as barras por cargas pontuais, em que a distância é o raio desse arco de circunferência, temos:
Substituindo os valores dados pelo enunciado: