Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 25.Exercícios e Problemas - Ex. 49
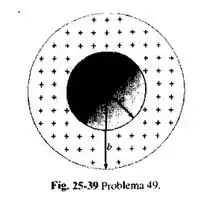
A Fig. 25-39 mostra uma casca esférica com densidade volumétrica de carga constante . Faça um gráfico mostrando a variação de com a distância ao centro da casca desde zero até . Suponha que , e .
Passo 1
Fala galera, bora lá! Antes de qualquer coisa, precisamos lembrar como se calcula o campo elétrico. Para , sabemos que, para uma esfera, a magnitude do campo é dado por
O invólucro esférico é um condutor, assim as cargas induzidas são desenvolvidas na superfície da casca. E o que isso significa?
Que não vai haver carga disponível no centro do invólucro e nem dentro do invólucro. Ou seja, quando teremos .
Passo 2
Para dar continuidade, nós vamos lembrar como calculamos a carga interna em uma casca esférica. A fórmula que nós usamos nesses casos é:
Substituindo na equação do no campo elétrico:
Assim,
Passo 3
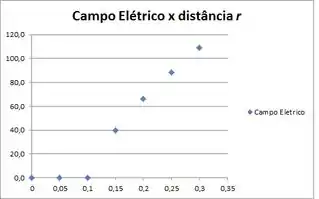
Faremos então um gráfico para representar a variação do campo elétrico com a distância , nos baseando na tabela abaixo.
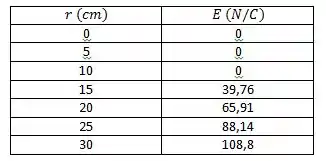
Percebemos que a teoria estava certa em relação à quando .
Resposta
