Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 34.Exercícios e Problemas - Ex. 6
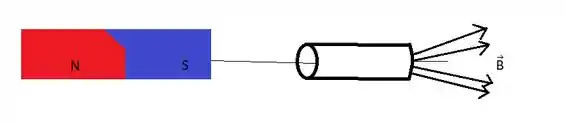
Enrolamos uma folha de papel formando uma superfície cilíndrica e, a seguir, colocamos esta superfície nas proximidades de uma barra imantada, como mostra a Fig. 34-20. (a) Esboce as linhas de campo B que atravessam o cilindro de papel,(b)Qual é o sinal de para cada dA deste cilindro de papel? (c) Existe alguma contradição com a lei do magnetismo de Gauss? Explique.
Passo 1
Eae galera!! Tudo bom? Vem comigo para mais um exercício.
- Como as linhas de campo de um ímã em forma de barra apontam na direção do polo Sul, as linhas de campo do desenho devem apontar para a esquerda na direção do fio,
- O sinal de em todos os elementos de área da superfície lateral do cilindro é negativo, pois o campo está saindo.
- Não, porque a lei de Gauss para o magnetismo se aplica apenas a superfícies fechadas. Se acrescentarmos as bases do cilindro para formar uma superfície fechada, a lei de Gauss será válida, pois o fluxo negativo através da superfície lateral do cilindro e da base do cilindro mais distante do ímã será compensado por um fluxo positivo na base do cilindro mais próxima do ímã.
Passo 2
Passo 3
Bora pro próximo.
Resposta
- Negativo.
- Não, porque a lei de Gauss para o magnetismo se aplica apenas a superfícies fechadas.
Exercícios de Livros Relacionados
Calcule a divergência e o rotacional do campo complexo E → x ,y ,z = E → 0e ik → ⋅ r → , onde E → 0 e k → são vetores constantes.
Sendo f r → e V → r → , respectivamente, um campo escalar e um campo vetorial, mostre que ∇ ⋅ f V → = f∇ ⋅ V → + V → ⋅ ∇ f
Mostre quegrad xx (grad xx vec u) = grad (grad * vec u) - ((del^2 vec u)/(del x^2) + (del^2 vec u)/(del y^2) + (del^2 vec u)/(del z^2))
Considere o campo u → x ,y ,z = zi ^ + xj ^ + yk ^ . Calcule sua divergência e seu rotacional.
Calcule a divergência e o rotacional do campo vec u (x , y , z) = x y z (hat i + hat j + hat k) .