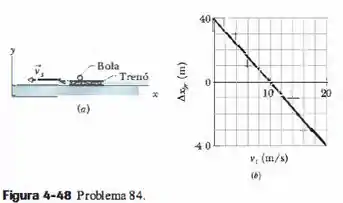
Na Fig.4-48a, um trenó se move no sentido negativo do eixo com uma velocidade escalar constante , quando uma bola de gelo é atirada do trenó com uma velocidade em relação ao trenó. Quando a bola chega ao solo, o deslocamento horizontal , em relação ao solo (da posição inicial à posição final) é medido. A Fig. 4-48b mostra a variação de , com . Suponha que a bola chegue ao solo na altura aproximada em que foi lançada. Quais são os valores (a) de , e (b) de ? O deslocamento da bola em relação ao trenó, , também pode ser medido. Suponha que a velocidade do trenó não mude depois que a bola foi atirada. Quanto é , para , igual a (c) e (d) ?

Como é um movimento de lançamento da bolinha, vamos ter a mesma coisa que tínhamos lá em lançamento oblíquo. No eixo x, temos um MU, já que não há aceleração; e no eixo y, temos um MUV, pois há aceleração da gravidade.

Então a posição em função do tempo para cada eixo é:

Eixo x:

Substituindo o valor da velocidade em relação ao solo, vamos ter que:

Eixo y:

Substituindo o valor da velocidade em relção ao solo, vamos ter que:

Agora, pensa aqui comigo, a variação da altura depois do voo completo é zero, pois ela vai e volta para a mesma altura (chão), então:

Show! Agora que já temos o tempo de voo, podemos achar e .

A variação da posição depois do voo é:

Olhando o enunciado, vemos que ele deu um gráfico da variação da posição do da bola em relação ao solo,. Isso é a mesma coisa que que nós achamos, então vamos compará-los.

Olhando para o gráfico dado, vemos que o coeficiente linear é

E o coeficiente angular é:

Substituindo 2 pontos:

:

:

Então:

A equação da reta fica então:

Voltando para a equação que achamos:

Temos que:

E

E

Agora queremos saber o para e .

Para descobrir a variação da posição da bola em relação ao trenó, temos que:

E se trata de um movimento uniforme:

Como vemos, , não depende de .

Então, para ambos, e , temos que vale: