Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.9 - Ex. 78

Um rio de 200   m de largura corre para leste com uma velocidade constante de 2,0   m / s . Um barco com uma velocidade de 8,0   m / s em relação à água parte da margem sul em uma direção 30 ° a oeste do norte. Determine (a) o módulo e (b) a orientação da velocidade do barco em relação à margem. (c) Quanto tempo o barco leva para atravessar o rio?

Passo 1

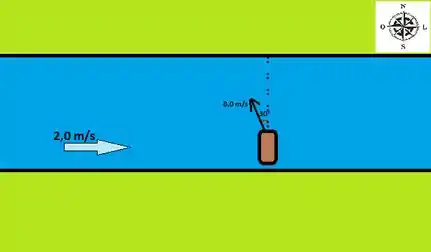
Galera, a velocidade do barco em relação a margem não é influenciada pela velocidade da água. A velocidade da água contribui apenas com a componente horizontal da velocidade do barco

Temos, que v B A = ( 8,0 ∠ 120 ° ) , em que o ângulo pode- se medir da forma convencional(no sentido anti-horário partindo do semieixo x positivo), logo, a notação dos vetores unitários

Na formula retangular , podemos obter que

v b = 8,0   m / s ⋅ c o s 30 ° = 6,9 3   m / s

v b = - 8,0   m / s ⋅ s e n   30 ° = - 4   m / s

v B M = v B A + v A M = 2.0   m / s i ^ + - 4.0 i ^ + 6.9 3 j ^ m / s = ( - 2.0 m / s ) i ^ + ( 6.9 3   m / s ) j ^

Logo

| v B M | = 7.2   m / s

A orientação de v B M é θ = tan - 1 ⁡ [ ( 2.0   m / s ) / ( 6.9 3   m / s ) ] = 16.16 ° (medido no sentido anti-horário partindo do semieixo x positivo) a oeste do norte.

Passo 2

Pessoal, sabemos que o barco tem uma velocidade v b = 6,9   m / s em relação margem e está a uma distância d = 200   m . Para descobrir quanto tempo leva para o barco fazer a Travessia vamos usar a fórmula V = Δ s Δ t isolando o Δ t :

V = Δ s Δ t   ⇒ t = Δ s v b = 200   m 6,9 3   m / s = 28.86   s ≅ 29 s

Resposta

a) | v B M | = 7.2   m / s

b) 16.16 ° (medido no sentido anti-horário partindo do semieixo x positivo) a oeste do norte.

c) 29   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A água de um rio se escoa com velocidade de 2,0m / s do norte para o sul. Um homem dirige um barco com motor ao longo do rio com velocidade igual a 4,2m / s em relação a água, de oeste para leste. A l
Dois trens passam pela mesma estação, sem parar nela, com dois minutos de diferença, ambos a 60 k m / h . O primeiro a passar viaja rumo ao sul e o segundo para o oeste. (a) Determine o vetor velocida
A distância entre as cidades A e B é l . Um avião faz uma viagem de ida e volta entre A e B , voando em linha reta, com velocidade V em relação ao ar. (a) Calcule o tempo total de voo, se o vento sopr
Um carro move-se para o leste com velocidade de 50,0 km/h. Pingos de chuva caem verticalmente em relação à Terra com velocidade constante. Os traços da chuva nas janelas laterais do carro fazem um âng
O piloto de um avião nota que a bússola indica o rumo para oeste. A velocidade escalar do avião em relação ao ar é de 150 km/h. O ar está se movendo com uma velocidade de 30,0 km/h em direção ao norte