Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 66

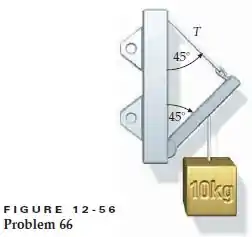
A Figura 12-56 mostra uma barra de 5,00 kg, com 1,00 m de comprimento, articulada em uma parede vertical e suportada por um arame fino. O arame e a barra forma um ângulo de 45° com a vertical. Quando um bloco de 10,0 kg é suspenso do ponto médio da barra, a tração T no arame suporte é 52,0 N. Se o arame se rompe quando a tração excede 75 N, até que distância da articulação o bloco pode ser suspenso?

Passo 1

Show galera ! Vamos começar o problema desenhando o que estamos vendo, mas vamos desenhar o nosso triângulo retângulo formado em uma perspectiva diferente:

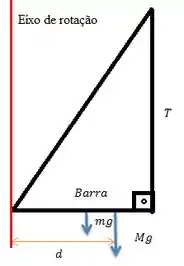
Sabemos que quando o corpo está em equilíbrio, as duas condições são satisfeitas:

∑ F → = 0     e   ∑ τ → = 0

Passo 2

Para achar a distância d máxima na qual o corpo de massa M deverá está pendurado para que a tração não exceda 75N, nós vamos usar a segunda condição, ∑ τ → = 0 .

O torque é calculado como:

∑ τ → = ∑ ( r → . F → )

Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher a lateral esquerda da barra, em contato com a parede, como nosso eixo.

Beleza ! Quando fazemos isso a força da gravidade terá r = L 2 , enquanto a tração terá r = L .

Já temos r agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força de tração é capaz de girar a barra no sentido anti-horário (+), já as forças peso giram no sentido horário (-).

Jogando toda informação na segunda condição:

L . T - L 2 F → g . B - d . F → g . C = 0

Substituindo as forças:

L . T - L 2 m g - d . M g = 0

O problema já nos deu as variáveis que iremos precisar:

L = 1,0   m

T = 75   N

m = 5,0   k g

M = 10,0   k g

g = 9,81   m / s ²

Na equação do torque:

( 1   m ) . ( 75   N ) - 1   m 2 ( 5,0   k g ) ( 9,81   m / s ² ) - d . ( 10,0   k g ) ( 9,81   m / s ² ) = 0

d = 0,83   m

Resposta

d = 0,83   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma viga rígida de 2,5 m de comprimento (Figura 12-51), suportada em seu centro no topo de um poste fixo de 1,25 m de altura, podendo pivotar sobre um mancal sem atrito. Uma extremidade da v
Uma prancha de 3,0m , com 5,0k g de massa, é articulada em uma de suas extremidades. Uma força F → é aplicada verticalmente sobre a outra extremidade, e a prancha forma um ângulo de 30 ° com a horizon
Um cilindro de massa M está apoiado sobre uma calha sem atrito, formada por um plano inclinado de 30 ° com a horizontal, à esquerda, e outro plano inclinado de 60 ° , à direita, como mostrado na Figur
Um corpo de 360 kg é suspenso por um arame preso a uma barra de aço de 15 m, que está articulada em uma parede vertical e suportada por um cabo, como mostrado na Figura 12-58. A massa da barra é 85 kg