Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 63
Um a caixa de 8,0 kg, de massa específica uniforme e duas vezes mais alta do que larga, é colocado sobre o piso de um caminhão. Qual é o maior coeficiente de atrito estático entre a caixa e o piso, tal que a caixa escorregará para a traseira do caminhão, ao invés de se inclinar, quando o caminhão acelerar para frente em uma estrada plana?
Passo 1
Vamos lá! Para começar nós vamos desenhar a caixa, como dito ela é duas vezes mais alta do que larga, ou seja:
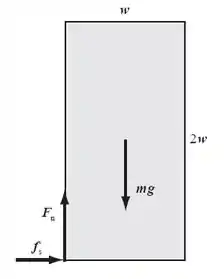
No centro de gravidade, ou seja, no ponto central da caixa, temos a força gravitacional sendo aplicada para baixo. Dada por:
Como nós temos duas superfícies em contato, existe a força normal perpendicular à superfície. Quando a placa está prestes a tombar agirá na borda da caixa, porque ela ficará apoiada somente neste ponto! E nessa situação as condições de equilíbrio ainda serão válidas.
Por último temos a força de atrito no caso da iminência do movimento, estas duas forças se relacionam:
O coeficiente de atrito estático máximo será:
Passo 2
É isso ai gente, já sabemos que nessa situação as condições de equilíbrio são válidas. Então podemos usar:
Calculado por
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher a lateral esquerda da caixa, onde está em contato com piso do caminhão.
Beleza ! Quando fazemos isso a força normal estará na posição . A força da gravidade terá enquanto a de atrito terá
Já temos r agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força de atrito é capaz de girar a barra no sentido anti-horário (+), já a força peso gira no sentido horário (-).
Substituindo :
Agora ficou fácil ! Jogamos na equação do coeficiente:
Passo 3
Não temos ainda, e para obtê-lo podemos usar a outra condição do equilíbrio, .
Como queremos a força normal, vamos analisar a direção y. O que temos? Apenas a força normal e a peso em direções opostas, ou seja:
Substituindo:
Concluímos então que quando 0,5 a caixa está na iminência de entrar em movimento, ou seja, de se inclinar. Valores acima deste indica que o corpo já está em movimento. Como queremos que a caixa deslize: