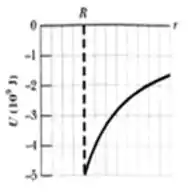
A Figura 13-42 mostra a função energia potencial de um projétil em função da distância da superfície de um planeta de raio R. Qual é a menor energia cinética necessária para que um projétil lançado da superfície “escape” do planeta?
Passo 1
Bom, pra entender a questão é necessário interpretar corretamente o gráfico. No eixo horizontal temos a distância entre o projétil e o centro do planeta. No eixo vertical temos a energia potencial gravitacional do projétil. Vemos que a medida que este se afasta do planeta a sua energia potencial diminuir. E a gente sabe também que a energia mecânica do sistema deve se conservar, já que não há dissipação de energia, Assim, toda a energia potencial vai virando energia cinética. Beleza. E a gente sabe também que para um projétil escapar gravitacionalmente de um planeta, ele deve ter energia cinética superior a energia potencial na superfície do planeta. Então, a gente tem