Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Questões Conceituais - Ex. 8
A velocidade de escape do Planeta X é de 10.000 m/s. O Planeta Y tem o mesmo raio do Planeta X, mas é duas vezes mais denso. Qual é a velocidade de escape do Planeta Y?
Passo 1
Nessa questão devemos entender dois conceitos:
- O que é a velocidade de escape;
- A conservação da energia mecânica.
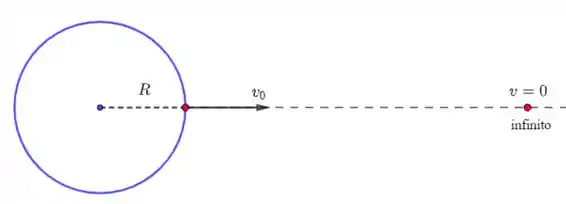
A velocidade de escape do campo gravitacional é a mínima velocidade necessária para que um corpo consiga se “livrar” do campo gravitacional de um planeta, chegando até o “infinito” com uma velocidade nula. Aqui, a palavra infinita quer dizer simplesmente uma distância muito grande entre o corpo e o planeta; essa distância é tal que podemos desprezar a interação gravitacional entre eles.
Quando fazemos o “lançamento” desse corpo, a energia mecânica irá se conservar! Isso ocorre, pois a força gravitacional é uma força conservativa. Sendo assim, podemos escrever que:
onde e indicam, respectivamente, a energia potencial e a energia cinética do corpo a ser lançado; os índices e indicam, respectivamente, o estado inicial e o estado final. Como dito acima, o estado final é o “infinito”, no qual . Logo,
A equação (embora aparentemente muito simples) vai nos dar a velocidade de escape do corpo!
Outra coisinha que devemos nos lembrar é o seguinte: o potencial gravitacional entre o planeta de massa e o corpo de massa é dado por:
onde é a distância entre o centro do planeta e o corpo.
Passo 2
Vamos aplicar o que foi discutido no passo 1. Temos que:
Logo,
Passo 3
No nosso problema, foi falado sobre a densidade, mas nada sobre a massa. Porém, podemos nos lembrar que:
onde é a densidade, é a massa e o volume da esfera, dado por . Logo,
Portanto, a equação da velocidade de escape poderá ser escrita como:
onde é uma constante! A escrevemos dessa maneira para facilitar nossas contas a seguir.
Passo 4
Para o planeta , temos que . Logo, temos que
Para o planeta , temos que e . Logo,
Resposta
A velocidade de escape do planeta é .