Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.6 - Ex. 55
Em , Galileu usou um telescópio que ele próprio havia cosntrúido para descobrir quatro satélites de Júpiter, cujos raios orbitais médios e períodos aparecem na tabela a seguir:
(a) Plote (eixo ) em função de (eixo e mostre que o resultado é uma linha reta. (b) Meça a inclinação da reta e compare-a com o valor previsto pela terceira lei de Kepler. (c) Determine a massa de Júpiter a partir da interseção da reta com o eixo .
Passo 1
A relação entre raios e períodos é dada pela 3ª lei de Kepler, vamos dar uma olhada na fórmula para entender o que estamos fazendo aqui:
A questão quer um gráfico onde aparece o , então vamos tirar o logaritmo dos dois lados pra ver no que dá:
Vamos sair usando as propriedades de logaritmo que sabemos:
A questão quer no eixo , então vamos isolar esse valor:
Essa é a “previsão teórica” das leis de Kepler. Vamos montar o gráfico agora.
Passo 2
Pegue uma calculadora. Converta a coluna do período para segundos (basta multiplicar cada número por , que é o número de segundos em um dia).
Depois, tire os logaritmos da tabela inteira.
Agora seria interessante pegar um papel milimetrado e fazer um gráfico para verificar a proposta do enunciado. A ideia é achar um gráfico parecido com esse:
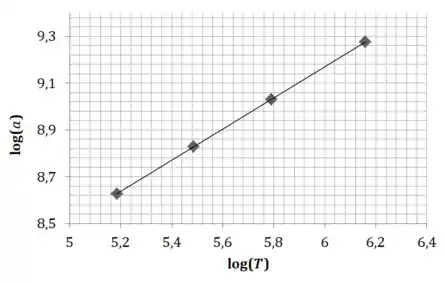
De fato, o resultado é uma linha reta. Está respondida a letra (a).
Passo 3
A letra (b) quer que a gente meça a inclinação do gráfico e compare com a previsão teórica da lei de Kepler. Bom, nós já vimos a previsão teórica, é essa fórmula aqui:
Como o é a variável do eixo , essa teoria prevê uma reta de inclinação . Vamos ver se bate com o nosso gráfico.
Você que fez o gráfico no papel milimetrado (parabéns pelo esforço!), deve agora escolher dois pontos e da sua reta (que não sejam os pontos que usamos pra traçar a reta), e anotar as coordendas deles. Depois fazer a seguinte conta:
Onde vai ser o coeficiente angular do gráfico. Com sorte vai dar alguma coisa perto de .
Outra opção é usar o método dos mínimos quadrados! Aplicando ele nesses pontos nós achamos esse valor para a inclinação da melhor reta:
Ou seja, um resultado muito bom! Está de acordo com a previsão da lei de Kepler.
Passo 4
O último passo é determinar a massa de Júpiter usando a interseção da reta com o eixo .
Vamos olhar de novo pra nossa fórmula:
Todas as quatro luas da tabela são de Júpiter e, portanto, orbitam Júpiter.
Isso quer dizer que esse na fórmula (que é a massa do corpo orbitado), é a massa de júpiter no nosso gráfico, que foi construído com os dados da tabela.
A questão pede para usarmos a interseção da reta com o eixo .
Olhando o seu gráfico, procure o ponto com . Vamos substituir isso na fórmula
Lembrando que e que :
No nosso gráfico, era aproximadamente (ocultamos essa parte para não prejudicar a visualização dos outros pontos). Isso significa que:
E olhando uma tabela vemos que a resposta correta é . Ou seja, ficamos bem próximos, uma margem de erro de .
Resposta
(b) A inclinação medida foi , que bate com a previsão da lei de Kepler
(c) A massa de Júpiter, calculada a partir do gráfico, é . Com erro relativo de .