A mesma corda descrita no Problema 1 está com uma extremidade amarrada num poste. A outra, inicialmente em repouso na posição de equilíbrio, é deslocada de para cima, com velocidade uniforme, entre e . A seguir, é deslocada para baixo, com a magnitude da velocidade reduzida à metade da anterior, entre e , quando retorna à posição de equilíbrio. (a) Desenhe a forma da corda no instante . (b) Desenhe a forma da corda no instante .
Passo 1
No Problema tínhamos uma corda em que as ondas se propagavam com ,
O enunciado diz que um pulso é gerado na extremidade solta da corda, que vamos chamar de .
Se o pulso é gerado com velocidade uniforme entre e , logo nesse último instante vamos ter algo assim no gráfico de :
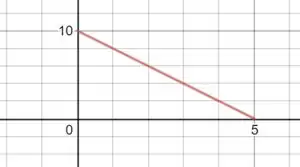
Obs.: O eixo vertical representa (em ) e o eixo horizontal representa (em )
Isso porque o pulso que se propaga a , então nos iniciais ele atinge no máximo a distânica .
E ele se comporta linearmente porque o deslocamento é produzido com velocidade uniforme.
Passo 2
Durante o próximo segundo, ou seja, entre e , o pulso se propaga pela seguinte distância:
Ao mesmo tempo, um deslocamento é produzido no sentido contrário (com a mesma amplitude de ), mas de forma duas vezes mais lenta.
Nesse caso teremos novamente uma linha reta, mas o coeficiente angular é dividido por e o seu sinal é trocado. Então, no instante , temos:
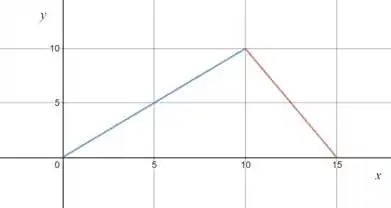
Pronto, agora acabaram os novos pulsos. Mas o que já está aí continua se propagando. Até o instante , ele terá andado:
Então em temos:
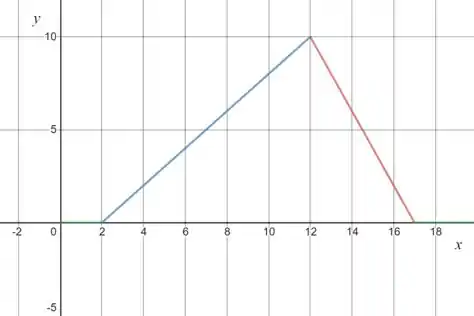
Passo 3
(b) Entre e , o pulso terá se movido pela seguinte distância:
Como a corda tem comprimento de , e em nosso pulso ia até os , os “frontais” do pulso serão refletidos.
Vamos começar simplesmente deslocando nosso pulso para a direita. Marcando o limite de da corda e ignorando a reflexão por enquanto:
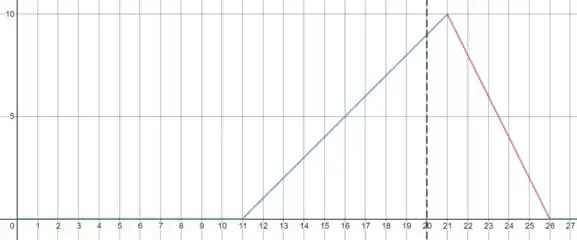
E agora simplesmente pegamos a parte que ficou para fora do limite, e invertemos a sua amplitude.
Depois deslocamos ela para trás, para representar a reflexão:
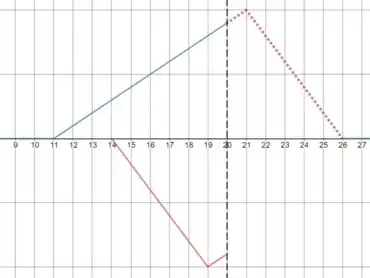
A parte pontilhada em vermelho representa a continuação imaginária do pulso.
Passo 4
Agora temos que fazer a superposição das ondas que restaram na corda.
Nesse caso, a superposição é apenas a soma dos valores de em cada ponto (contar os quadrados no quadriculado já é suficiente).
Fazendo isso chegamos no seguinte resultado (a linha preta contínua representa a onda resultante):
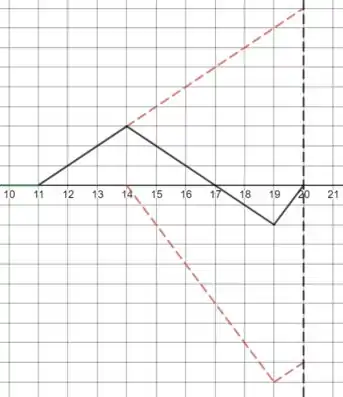
Resposta
(a) Ver desenho.
(b) Ver desenho.