Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 16.Problemas Desafiadores - Ex. 83
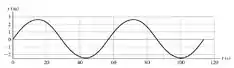
A Figura 16.45 mostra a flutuação de pressão de uma onda sonora não senoidal em função de para . A onda se propaga no sentido .a) Faça o gráfico da flutuação de pressão em função de para . Mostre pelo menos dois ciclos de oscilações. b) Faça um gráfico do deslocamento nessa onda sonora em função de para . No ponto , o deslocamento para é igual a zero. Mostre pelo menos dois comprimentos de onda da onda.c) Faça um gráfico do deslocamento em função de para . Mostre pelo menos dois ciclos de oscilações. d) Descreva como o cone de um alto-falante deve se mover em função do tempo para produzir a onda sonora desse problema.
Passo 1
A fase da onda é determinada pelo valor de , portanto t aumentando é equivalente a
diminuindo com t constante. A flutuação e o deslocamento da pressão estão relacionados pela equação:
Bom,
Se versus é uma linha reta, então versus versus x é uma parábola.
Para o ar: .
Passo 2
- Vamos então, esboçar o gráfico:
- Da equação, a função que tem o dado em é dada graficamente na Figura a seguir:
- Supondo que uma onda se mova na direção , é como mostrado a seguir:
- A velocidade máxima de uma partícula ocorre quando uma partícula está se movendo através da origem e a velocidade da partícula é
- O cone do alto-falante se move com o deslocamento conforme encontrado na parte (c); o cone do alto-falante alterna entre movimento para frente e para trás com magnitude constante de aceleração (mas sinal de mudança). A aceleração em função do tempo é uma onda quadrada com amplitude de e frequência
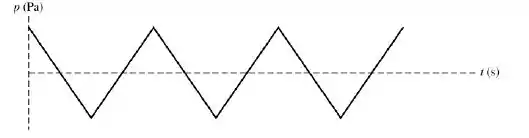
Passo 3
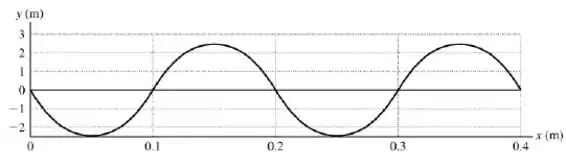
Cada seção é uma parábola, não uma parte de uma curva senoidal.
O período é :
e a amplitude é igual à área sob a curva versus entre e dividido por , ou .
Passo 4
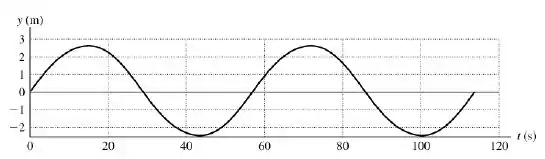
Passo 5
A velocidade máxima é encontrada a partir da pressão máxima e
A aceleração máxima é o gradiente máximo de pressão dividido pela densidade,
Passo 6
Podemos verificar que versus tem uma forma proporcional à inclinação do gráfico de versus . O mesmo se aplica aos gráficos versus.
Resposta
