a) Defenda a seguinte afirmação: “Em cada onda sonora senoidal, a variação da pressão dada pela Equação (16.4) atinge o valor máximo quando o deslocamento dado pela Equação (16.1) é igual a zero”. b) Para uma onda sonora senoidal dada pela Equação (16.1), com amplitude e comprimento de onda , faça um gráfico do deslocamento e da flutuação de pressão em função de para . Mostre pelo menos dois comprimentos de onda em seus gráficos. c) O deslocamento em uma onda sonora não senoidal é mostrado na Figura 16.42 em função de para . Faça um gráfico mostrando a flutuação de pressão dessa onda em função de para . Essa onda sonora possui a mesma amplitude de da onda do item . Ela possui a mesma amplitude de pressão? Justifique são resposta. d) A afirmação do item (a) é necessariamente verdadeira quando a onda sonora não for senoidal? Explique seu raciocínio.
Passo 1
a) A gente pode dizer que onde existe um nó de deslocamento , o ar está comprimido ou rarefeito naquele ponto, por isso, a pressão vai ser máxima, dessa forma, onde existe ventre de pressão, existe nó de deslocamento e vice-versa.
Passo 2
b) Com o valor dado do comprimento de onda , podemos calcular o número de onda para podermos montar o gráfico. Com , a equação da onda fica:
Sendo que é:
Com o valor de comprimento de onda dado :
Substituindo esse valor e a amplitude do enunciado:
O gráfico então fica (vamos multiplicar a escala em por e dividir a escala em por 25, porque senão as ondas irão ficar muito juntas e vai ficar difícil visualizar):
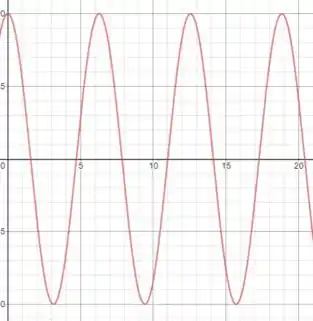
Para a amplitude de pressão, a equação vai ficar parecida, mas com a função seno no lugar:
O gráfico fica:
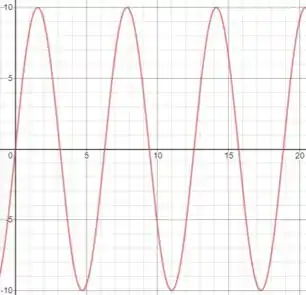
Passo 3
c) O gráfico de flutuação da pressão vai ter a seguinte cara:
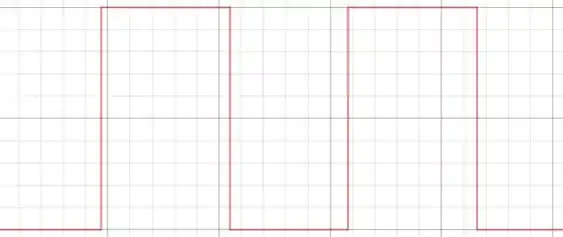
A amplitude de pressão não será a mesma, porque como a amplitude de pressão é a derivada de da equação da função de deslocamento da onda, e a onda da letra (c) é diferente da letra (b), as amplitudes serão diferentes.
Passo 4
d) Quando ocorre um nó de deslocamento em uma função diferente não senoidal, o máximo de pressão não necessariamente será nesse nó, como podemos ver pela letra (c), a pressão atinge seu máximo antes do nó do gráfico dado na questão, e depois dele ela continua seu valor máximo até cair.
Resposta
Ei, a resposta está no passo a passo :)