Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.Problemas Adicionais - Ex. 68
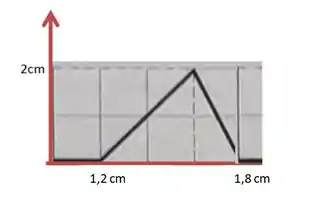
Um pulso isolado, cuja forma de onda é dada por , com em centímetros e em segundo, é mostrado na figura para . A escala do eixo vertical é definida por . Qual é (a) a velocidade e (b) o sentido de propagação do pulso? (c) Plote em função de para . (d) Plote em função de para .
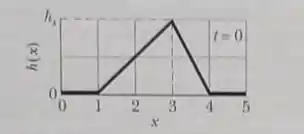
Passo 1
- Aqui, como em toda questão de física, precisamos lembrar da teoria! Lembre-se que uma onda progressiva deve ser representada por uma equação , tal que representa qualquer função (qualquer mesmo). Nesse caso, a gente tem que e .
- Lembra que, sempre que o sinal de é negativo na equação da onda, isso quer dizer que ela se move no sentido positivo do eixo ? Pois é o que ocorre nesse caso! A onda move-se no sentido positivo de .
- Veja que em a onda terá percorrido certo deslocamento horizontal para a direita igual a . Então, o desenho desse padrão de onda após esse intervalo de tempo pode ser representado pela imagem abaixo:
- A parte mais à direita da onda atinge em um intervalo de tempo igual a . Além disso, essa abscissa atinge um ponto de máximo quando . Com base nisso, podemos plotar o seguinte gráfico:
Como , temos:
Passo 2
Passo 3
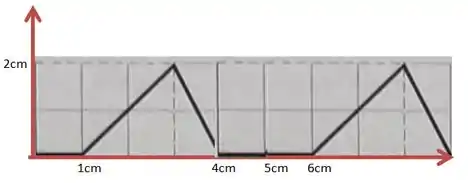
Passo 4
Resposta
Exercícios de Livros Relacionados
Quando um projétil veloz, como uma bala ou um fragmento de bomba, atinge um colete moderno à prova de balas , o tecido do colete detém o projétil e impede a perfuração dispersando rapidamente a energi
O tipo de borracha usada em algumas bolas de beisebol e de golfe obedece a lei de Hooke numa ampla faixa de alongamentos.Uma tira desse material tem comprimento λ e massa m . Quando uma força F é apli
Uma onda senoidal é produzida em uma corda com uma massa específica linear de 2,0g / m . Enquanto a onda se propaga, a energia cinética dos elementos de massa ao longo da corda varia. A figura ( A ) m
a) Defenda a seguinte afirmação: “Em cada onda sonora senoidal, a variação da pressão dada pela Equação (16.4) atinge o valor máximo quando o deslocamento dado pela Equação (16.1) é igual a zero”. b)
A Figura 16.45 mostra a flutuação de pressão P de uma onda sonora não senoidal em função de x para t = 0 . A onda se propaga no sentido + x .a) Faça o gráfico da flutuação de pressão P em função de t