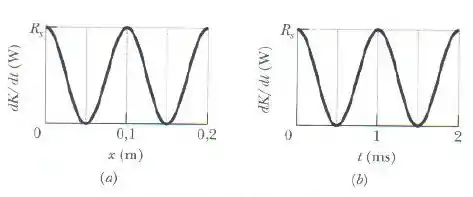
Uma onda senoidal é produzida em uma corda com uma massa específica linear de . Enquanto a onda se propaga, a energia cinética dos elementos de massa ao longo da corda varia. A figura mostra a taxa com a qual a energia cinética passa pelos elementos de massa da corda em um certo instante em função da distância ao longo da corda. A figura é semelhante, exceto pelo fato de que mostra a taxa com a qual a energia cinética passa por um determinado elemento de massa (situado em um certo ponto da corda) em função do tempo . Nos dois casos, a escala do eixo vertical é definida por . Qual é a amplitude da onda?
Passo 1
Belezera galerinha, primeira coisa precisamos lembrar da fórmula que nos dá a energia cinética em um ponto da corda:

Já que a onda é senoidal, a função do deslocamento é essa aqui:
E a função da velocidade transversal é simplesmente a derivada dessa equação em relação ao tempo:

Agora, a energia cinética segue a fórmula:
Mas como não dá pra falar na “massa de um ponto” da corda, vamos falar de “pedaços bem pequenos da corda”, ou seja, vamos usar diferenciais, onde um pedacinho infinitesimal de massa é dado como:
Onde é a massa específica da corda, enquanto é um pedacinho infinitesimal de corda.
E então a fórmula da energia cinética fica assim:
Tá, agora vamos dividir isso por , já que a grandeza representada no gráfico é :

E aquele é simplesmente a velocidade de propagação da onda, de forma que:
Passo 2
Ok pessoal, foi difícil, mas achamos a função que está representada nos gráficos. É essa aqui:
Agora, qual a primeira coisa que podemos extrair aqui? Bom, o ponto de máximo dos dois gráfico é:
E olhando pra função, qual o valor máximo que ela atinge? Como o cosseno ao quadrado varia entre e , o valor máximo é:
E então, igualando esse máximo, com o valor extraído do gráfico obtemos que:
E assim chegamos em uma fórmula pra amplitude, que afinal de contas é o que queremos calcular! Isolando :
Tal que:

Passo 3
Beleza, agora só está falando saber a velocidade e a frequência angular, porque a massa específica já foi dada, é:
Tem alguma informação no gráfico que pode ajudar a gente a calcular a velocidade e a frequência?

Sim! O período e o comprimento de onda. Perceba que o que define esses valores no gráfico é o que está dentro do cosseno ou do seno, e esses valores não mudam quando nós derivamos.
Ou seja, o período e o comprimento de onda observados no gráfico do enunciado são os mesmos da onda.

Obs.: Cuidado, como o cosseno fica ao quadrado na função do gráfico, a parte que normalmente seria negativa é “jogada” pra cima pois se torna positiva ao ser elevado ao quadrado, mas é sempre preciso contar dois picos pra achar o período ou o comprimento de onda. Logo:
Isso quer dizer que a frequência angular é:
E a velocidade é:

Passo 4
Agora vamos substituir tudo na equação da amplitude :
Logo:
Então:
Ou em :
Pronto!
Resposta
A amplitude é .