Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas Desafiadores - Ex. 74
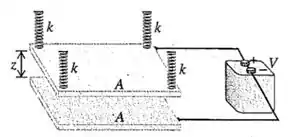
O capacitor com placas pararelas imerso no ar indicado na figura 24.40 possui duas placas condutoras de área . A placa inferior repousa sobre um suporte fixo e a placa superiore está suspensa por quatro molas, com constante , colocadas nos quartro vértices da placa, como mostra a figura. Quando descarregadas, as placas são separadas por uma distancia . Uma bateria é ligada, produzindo uma diferença de potencial V entre as palcas. Isso faz a distância entre as placas diminuir para z. Despreze os efeitos nas bordas das placas. (a)Mostre que a força eletrostática entre as placas carregadas possui módulo . (Dica: Veja o exercício 24.29.) (b) Obtenha uma expressão que relacione a distância z a diferença de potencial V. A equação resultante será uma equação cúbica em z. (c) Dados os valores , , e , calcule os dois valores de para os quais a placa do topo permanece em equilíbrio. (d) Para cada um dos valores de z encontrados na parte (c), verifique se o equilíbrio é estável ou instável, Para o equilíbrio estável, um pequeno deslocamento do objeto dá origem a uma força restauradora, que força o objeto a voltar para a posição de equilíbrio. Para o equilíbrio instável, um pequeno deslocamento dá origem a uma força resultante que faz o objeto se afastar da posição de equilíbrio.
Passo 1
A força em uma placa é devido ao campo elétrico da outra placa. A força eletrostática deve ser equilibrada pelas forças nas molas. O campo elétrico de uma placa é 
Passo 2
(a) A força entre duas placas pararelas, é:
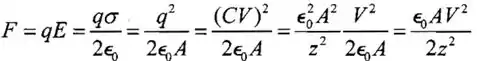
(b)Quando V=0, a separação é somento . Quando a tensão é diferente de 0, a força total das 4 molas é igual a força eletrostática calculada no item (a).
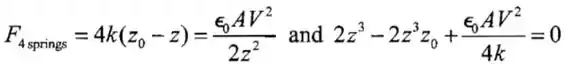
Passo 3
(c)Para , , e então,
As soluções físicas possíveis para isso são e
Passo 4
(d) O equilíbrio estático ocorre se um pequeno deslocamento do equilíbrio gera uma força voltando para o ponto de equilibro.