A figura 21-46 mostra um haltere que consiste em duas partículas pequenas idênticas, cada uma com massa , presas à extremidades de um bastão fino (sem massa) de comprimento que pode girar em torno de um ponto que passa pelo seu centro. As partículas têm cargas e , e o haltere está localizado em um campo elétrico uniforme . Mostre que, para pequenos valores do ângulo entre a direção do dipolo e a direção do campo elétrico o sistema começa a mover-se em movimento harmônico simples e obtenha uma expressão para o período de tal movimento.
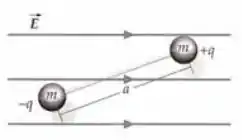
Passo 1
Veja a figura abaixo, onde é um ângulo pequeno.
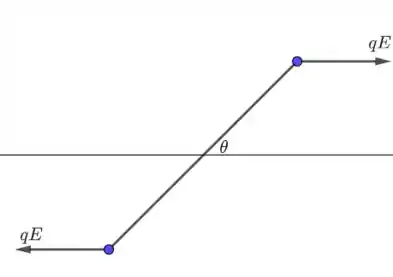
Vamos calcular o torque em torno do centro de massa do sistema.
Notemos que esse torque tende a trazer o dipolo de volta para a posição onde . Sendo assim, podemos colocar o sinal negativo no torque:
Mas, sendo um ângulo pequeno, temos que . Além disso, , sendo o momento de inércia, e . Logo,
Agora, vamos calcular :
Portanto,
Passo 2
Identificamos a equação acima como sendo a equação característica de um MHS:
assim,
Passo 3
Agora, ficou fácil calcular o período:
Resposta
O período vale .