Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.Problemas Adicionais - Ex. 67

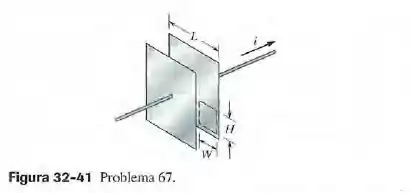
Na figura 32-41, um capacitor de placas paralelas está senti descarregado por uma corrente i = 5,0   A . As placas são quadrados de lado L = 8   m m . (a) Qual é a taxa de variação do campo elétrico entre as placas? (b) Qual é o valor de ∮ B → . d s → ao longo da linha tracejada, na qual H = 2,0   m m e W = 3,0   m m ?

Passo 1

Levando em conta que o capacitor está sendo descarregado, vamos utilizar a equação da corrente de deslocamento, que é representada pelo símbolo i d :

i d = - ε o d ϕ E d t

i d = - ε o A d E d t

Vamos explicitar d E d t na equação acima:

d E d t = - i d ε o A

Agora que conseguimos a expressão que queríamos, vamos substituir os valores que foram dados no enunciado!

d E d t = - 5,0   A 8,85 × 10 - 12 C 2 N . m 2 0,0080   m 2

d E d t = - 8,8 × 10 15   V / m   . s

Passo 2

A integral ∮ B → . d s → é dada por:

∮ B → . d s → = μ o i d , e n v

Para pontos situados no interior do capacitor, a curva de integração envolve apenas uma parte i d . e n v da corrente i d . Vamos supor que i d está distribuída uniformemente ao longo da área das placas. Nesse caso, a parte da corrente de deslocamento envolvida pela curva é proporcional à área envolvida pela curva:

i d , e n v = i d á r e a   e n v o l v i d a á r e a   t o t a l

Substituindo este valor na integral anterior, temos:

∮ B → . d s → = μ o i d á r e a   e n v o l v i d a á r e a   t o t a l

Uma vez que temos a expressão para o problema, só nos resta substituir os valores e correr pro abraço!

∮ B → . d s → = μ o i d á r e a   e n v o l v i d a á r e a   t o t a l

∮ B → . d s → = μ o i d 2 , 0 × 10 - 3   m 3 , 0 × 10 - 3   m 64 × 10 - 6   m ²

∮ B → . d s → = 5 , 9 × 10 - 7   W b / m

Resposta

  1. d E d t = - 8,8 × 10 15   V / m   . s ;
  2. ∮ B → . d s → = 5,9 × 10 - 7   W b / m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 29-71, um cano circular longo de raio externo R = 2,6c m conduz uma corrente (uniformemente distribuída) i = 8,00m A para dentro do papel. Existe um fio paralelo ao cano a uma distância de 3
A figura 29-67 mostra duas curvas fechadas que envolvem duas espiras que ocnduzem correntes i 1 = 5,0A e i 2 = 3,0A . Determine o valor da integral ∮ B → . d S → (a) para a curva 1 e (b) para a curva
A densidade de corrente J no interior de um fio cilíndrico longo de raio a = 3,1m m é paralela ao eixo central e o módulo varia linearmente com a distância radial r de acordo com a equação J = J o r /
Dois fios longos estão no plano x y e conduzem correntes no sentido positivo do eixo x . O fio 1 está em y = 10,0c m e conduz uma corrente de 6,00A ; o fio 2 está em y = 5,00c m e conduz uma corrente
A figura 29-79 mostra uma seção reta de um condutor cilíndrico longo de raio a = 4,00c m que contrém um furo cilíndrico de raio b = 1,50c m . Os eixos centrais do cilindro e do furo são paralelos e es