Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 11

A Figura 23.17 mostra uma barra metálica de resistência elétrica desprezível, em forma de U, posicionada na vertical, à qual se prende uma barra horizontal de resistência elétrica R . Os anéis que prendem a barra horizontal à barra metálica permitem que aquela deslize na vertical com atrito desprezível. A massa do conjunto barra horizontal mais os anéis vale m . Um campo magnético horizontal de intensidade uniforme B cobre toda a região do sistema.

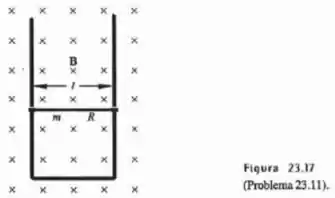
A barra inicia seu deslizamento a partir do repouso. (a) Qual é o sentido da corrente induzida? (b) Qual é a força magnética sobre a barra? (c) Escreva a equação de movimento da barra. (d) Mostre que a velocidade terminal da barra é

v m a x = m g R l B 2

Passo 1

Fala galerinha, beleza?

Esse exercício é um dos mais clássicos sobre lei de Faraday! A ideia básica é que conforme a barra cai o fluxo magnético vai variar, de modo que vai parecer uma fem induzida e uma corrente no circuito.

Primeiro vamos definir um sistema de coordenadas:

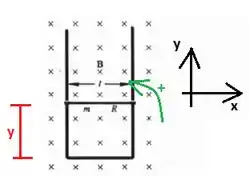
Repare que o eixo z aponta para fora da tela, de modo que B → = - B   z ^ . Pela regra da mão direita, o sentido positivo de corrente é o anti-horário, marcado em verde na figura.

O fluxo magnético será

Φ B = ∫ B → ⋅ n ^   d A

Como n ^ = z ^ e B → = - B   z ^ , temos que

Φ B = - B A = - B l y

Pela lei de Faraday, a fem induzida será

E = - d Φ B d t = B l d y d t

Aqui vem o pulo do gato:

v = - d y d t

A velocidade da barra é o negativo da derivada temporal de y . O sinal de menos aparece pois conforme y diminui a velocidade é positiva! Com isso, achamos

E = - B v l < 0

Como a fem é negativa, a corrente flui no sentido oposto ao convencionado pela regra da mão direita (verde no desenho). Logo, a corrente flui no sentido horário.

Passo 2

Usando a lei de Ohm, achamos

R I = B v l → I = B v l R

A força magnética que atua sobre a barra será

F → = I l   x ^ × - B   z ^ = B I l   y ^

Substituindo a expressão da corrente:

F → = B 2 l 2 v R   y ^

Passo 3

Para escrever a equação de movimento nós analisamos as forças que agem sobre a barra: peso e força magnética:

m   a → = B 2 l 2 v R   y ^ - m g   y ^

Assim,

a = B 2 l 2 v m R - g

Como a = d v / d t , temos que

d v d t = B 2 l 2 m R   v - g

Para encontrar a expressão da velocidade terminal fazemos

d v d t → 0

Assim,

B 2 l 2 m R   v m a x - g = 0

Portanto,

v m a x = m g R B 2 l 2

Com isso nós finalizamos o problema 😉.

Resposta

Horário.

F → = B 2 l 2 v R   y ^

d v d t = B 2 l 2 m R   v - g

v m a x = m g R B 2 l 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bobina supercondutora tem 15000 espiras, raio interno de 2,0c m , raio externo ligeiramente superior a 2c m e comprimento de 10c m . (a) Qual é o valor da voltagem a ser aplicada à bobina para que
Mostre, a partir das Eqs. 33-11 e 33-17, que E ( x , t ) e B ( x , t ) , o campo elétrico e o campo magnético associados a uma onda eletromagnética, devem satisfazer as “equações de onda”: ∂ 2 E ∂ t 2
(a) Mostre que as Eqs. 33-1 e 33-2 satisfazem as equações de onda do Problema 108. (b) Mostre que expressões da forma E = E m f ( k x ± ω t ) e B =B m f ( k x±ω t ) , em que f ( k x±ω t ) é uma função
Usando a aproximação do campo do dipolo para o campo magnético da Terra dada no Problema 13. calcule a intensidade máxima do campo magnético na fronteira do revestimento do núcleo, que se encontra a 2
O fluxo magnético através de cinco faces de um dado vale Φ B = ± NW b onde 1 ≤ N ≤ 5 é o número de pomos sobre cada face. O fluxo é positivo (para fora) para N par e negativo (para dentro) para N ímpa