Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 10
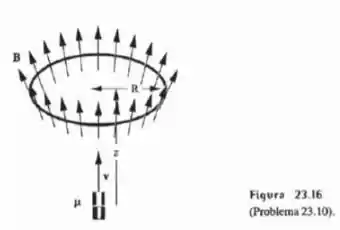
Um ímã se aproxima de um anel, movendo-se sobre o eixo deste. A Figura 23.16 mostra a situação em um dado instante em que o centro do anel está a distância do centro do ímã. Nota-se a simetria axial do campo magnético no plano do anel.
Utilizando a aproximação de dipolo para o campo magnético, mostre que
a) o seu fluxo na superfície contornada pelo anel vale
b) para , esta expressão se aproxima para
c) a fem no anel vale
Passo 1
Fala galerinha, beleza?
Esse problema é daqueles mais complicadinhos que faremos bastante conta...
Temos um ímã, que vamos aproximar por um dipolo, cujo campo magnético atravessa um anel, como mostrado na figura. Primeiro queremos calcular o fluxo do campo magnético sobre esse anel.
Observe que o versor normal ao anel aponta na direção , de modo que
Vamos olhar com atenção para o campo magnético produzido por um dipolo na direção :
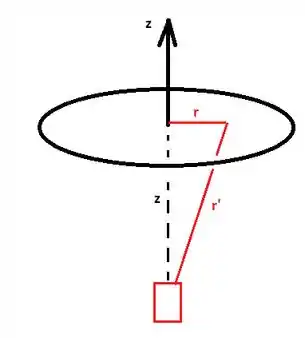
Na equação 22.21 do livro temos, em termos de e :
Mas note que por Pitágoras:
Assim, podemos escrever o campo magnético em termos de :
Passo 2
Temos que integrar essa última expressão em com indo de até :
O trabalho duro agora é fazer essa integral! Vamos fazer a mudança de variável
Assim,
Daí é só fazer a integral:
Juntando os termos achamos exatamente a expressão dada no enunciado:
Passo 3
No item (b) vamos fazer a aproximação . Para isso usaremos a aproximação binomial:
Assim,
Portanto,
Analogamente,
Com isso, temos que
Portanto,
Passo 4
Por fim, no item (c) queremos achar a fem no anel. Para isso, usamos a lei de Faraday:
Você precisa observar que a única grandeza que varia com o tempo é de modo que pela regra da cadeia:
A derivada do primeiro termo será
Já para o segundo termo:
Assim,
Com isso,
Logo,
Mas como , temos que
UFA! Terminamos o problema 😉.
Resposta
Demonstração.