Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 7
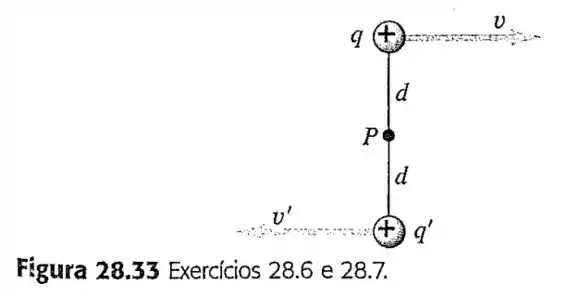
7- A figura mostra duas cargas puntiformes, e , que se movem em relação a um observador situado no ponto . Suponha que a carga inferior seja negativa, com .
Calcule o módulo, a direção e o sentido do campo magnético resultante que elas produzem no ponto quando ; .
Determine a direção e o sentido da força magnética que a carga exerce sobre e a direção e o sentido da força magnética que exerce sobre .
Para qual é a razão entre o módulo da força magnética entre as cargas e o módulo da força de Coulomb que existe entre as cargas?
Passo 1
Utilizando a fórmula que descobrimos no passo anterior para essa questão, nós descobrimos de forma vetorial que :
Agora você vai entender por que quase sempre é válido fazer da forma vetorial, por que nele já temos o módulo e o sentido em uma conta só.
Onde nessa questão temos logo:
Em teremos:
Campo esse que entrará na página
Para nós vamos ter:
E em :
Campo esse que vai sair da página, pois agora temos como sentido.
Passo 2
Fazendo a força magnética igual a:
Nós teremos:
Contando o campo magnético que faz em . Então:
E a distância agora não vai ser da carga até e sim da carga até a outra.
Isso nos diz que a força magnética em aponta para baixo, sendo uma força de atração.
Passo 3
A força elétrica entre as duas cargas é de:
Então a razão entre as duas forças será:
Ai não entendi o que ele quis dizer com Para porém a razão entre os dois é essa aí para e