Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.3 - Ex. 35
A figura 29-63 mostra o fio 1 em seção reta; o fio é retilíneo e longo, conduz uma corrente de para fora do papel e está a uma distância de uma superfície. O fio 2, que é paralelo ao fio 1 e também longo, está sobre a superfície a uma distância horizontal do fio 1 e conduz uma corrente de para dentro do papel. Qual é a componente da força magnética por unidade de compriento que age sobre o fio 2?
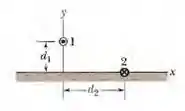
Passo 1
Fala aí! como vai? 😉
Nesse problema temos dois fios... a distancia vertical entre eles é e a distancia horizontal é . o fio 1 é percorrido por uma corrente para fora do papel e o fio 2 para dentro do papel. A partir daí queremos saber qual é a componente da força magnética por unidade de compriento que age sobre o fio 2.
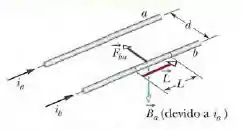
A força entre duas correntes paralelas na presença do campo magnético externo é dada por:
em que é o vetor comprimento do fio. Podemos ver na figura acima, os vetores e são mutuamente perpendiculares e, portanto, de acordo com a equação para fios retilíneos longos, podemos escrever:
Onde e são as correntes dos fios, é a permissividade magnética do vácuo, é o comprimento e a distancia entre os fios.
Veja só! 🤔
Passo 2
Podemos usar essa equação do passo anterior para calcular o módulo da força entre os fios e a componente correspondente a multiplicar o módulo por . Assim, a componente da força por unidade de comprimento é:
Substituindo os valores do problema, temos
E aí! entendeu tudo? Responde Aí! 😉
Resposta
A componente é igual a: