Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 67
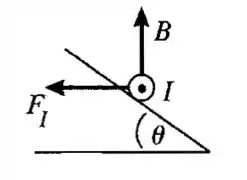
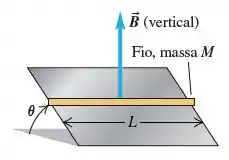
Um fio retilíneo condutor de massa M e comprimento L é colocado sobre um plano inclinado sem atrito, formando um ângulo com a horizontal (Figura 27.61). Existe um campo magnético vertical uniforme ao longo de todos os pontos (produzido por um conjunto de eletroímãs não indicados na figura). Para impedir que o fio escorregue para baixo do plano, uma fonte de tensão é aplicada nas extremidades do fio. Quando uma corrente com um valor preciso circula no fio, ele permanece em repouso. Determine o módulo e o sentido da corrente que circula para fazer o fio ficar em repouso. Copie a figura e desenhe o sentido da corrente em seu desenho. Além disso, faça um diagrama de corpo livre mostrando todas as forças que atuam sobre o fio.
Passo 1
Pelo desenho temos que as únicas forças que atuam no fio são a força magnética, a força peso e a normal.
A força peso está direcionada para o centro da Terra e faz um ângulo com o eixo .
A força magnética está entrando no plano e faz um ângulo com o eixo .
E a força normal é perpendicular a superfície de contato.
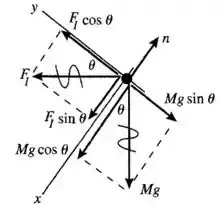
Passo 2
Como queremos a corrente que faz com que o fio fique em repouso:
Temos então:
Isolando a corrente:
Como o fio e o campo magnético são perpendiculares .
Passo 3
Considerando que a corrente é perpendicular ao campo magnético e a força magnética, temos então que o sentido da corrente será da esquerda para a direita.
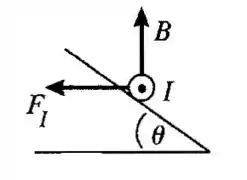
Resposta
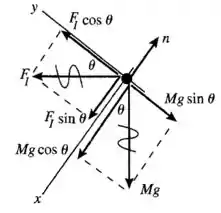
A corrente está da esquerda para a direita.
