Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 71d
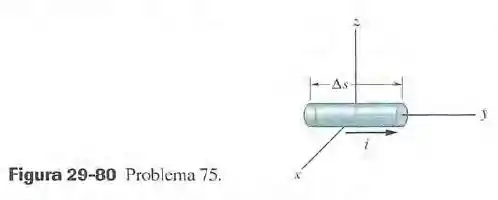
A figura 29-80 mostra um segmento de fio de comprimento , com o centro na origem, percorrido por uma corrente no sentido positivo do eixo (como parte de um circuito completo). Para calcular o módulo do campo magnético produzido pelo segmento em um ponto situado a vários metros da origem, podemos usar a lei de Biot-Savart na forma , já que e podem ser consideradas constantes para todo o segmento. Calcule (em termos dos vetores unitários) para pontos situados nas seguintes coordenadas: (d) .
Passo 1
De acordo com a lei de Biot-Savart,
Para e , temos:
na qual foram usadas as relações , e Assim, a equação anterior se torna
Passo 2
O campo no ponto é:
Resposta
O campo é:
Exercícios de Livros Relacionados
A figura 29-80 mostra um segmento de fio de comprimento ∆ s = 3,0c m , com o centro na origem, percorrido por uma corrente i = 2,0A no sentido positivo do eixo y (como parte de um circuito completo).
A figura 29-83 mostra uma seção reta de uma placa condutora infinita que conduz uma corrente λ por unidade de largura, dirigida para fora do papel. (a) Use a lei de Biot-Savart e a simetria da situaçã
Mostre que o módulo do campo magnético produzido no centro de uma espira retangular de comprimento L e largura W , percorrida por uma corrente i , é dado por: B = 2 μ o i π ⋅ L 2 + W 2 1 2 L W
Uma espira quadrada de lado a conduz uma corrente i , Mostre que, no centro da espira, o módulo do capo elétrico produzido pela corrente
Na figura 29-63, cinco fios paralelos longos no plano x y estão separados por uam distância d = 50c m . As correntes para dentro do papel são i 1 = 2,00A , i 3 = 0,250A , i 4 = 4,00A e i 5 = 2,00A ; a