É impossível existir um campo elétrico uniforme que caia repentinamente até zero em uma região do espaço onde o campo magnético é uniforme e constante. Para provar essa afirmação, use o método da contradição. Suponha que essa hipótese seja verdadeira, a seguir mostre que ela contradiz uma lei da natureza.

Na metade inferior de uma folha de papel, desenhe retas paralelas igualmente espaçadas para representar um campo elétrico uniforme, orientado da esquerda para a direita. Use linhas tracejadas para representar um retângulo com um lado paralelo ao campo elétrico e o outro lado paralelo do retângulo fora do campo elétrico, em que .

Mostre que a integração ao longo do retângulo contradiz a lei de Faraday, equação .

Como é inviável desenhar o problema seguindo exatamente as instruções do enunciado, mas vamos desenhar a região do campo elétrico da qual trata o problema que pode ser esquematizada da seguinte forma

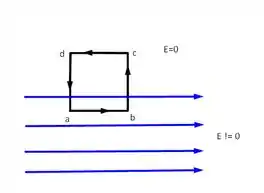
Devemos lembrar que a lei de Faraday para esse caso dada por

Como temos constante isso implica que , então vamos ter reduzido a

Aplicando a situação do problema teremos

Mas fazendo isso nós iremos ter , assim, , porém, desde que assumimos que o resultado obtido contradiz a Lei de Faraday. Assim, não podemos ter que um campo elétrico uniforme abruptamente caia para zero em uma região na qual o campo magnético é constante.