Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.5 - Ex. 32

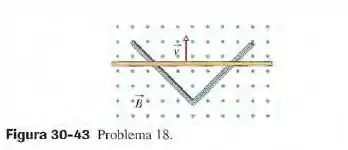
Na figura 30-43, dois trilhos condutores retilíneos formam um ângulo reto. Uma barra condutora em contato com os trilhos parte do vértice no instante t = 0 com uma velocidade escalar constante de 5,20   m / s e passa a se mover entre os trilhos. Um campo magnético B = 0,350   T , dirigido para fora da página, existe em toda a região. Determine (a) o fluxo magnético através do triângulo formado pelos trilhos e a barra no instante t = 3,00   s e (b) a força eletromotriz aplicada ao triângulo e a barra nesse instante. (c) Se a força eletromotriz é dada por ε = a t n , em que a e n são constantes, determine o valor de n .

Passo 1

Bom, galera, o módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:

ε = - d ϕ B d t

O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.

A altura do triângulo formado pelos trilhos e pela barra no instante t é igual à distância percorrida pela barra até esse instante: d = v t , na qual v é a velocidade da barra. A base do triângulo (distância entre os pontos de interseção da barra com os trilhos) é 2 d . Assim, a área do triângulo é:

A = 1 2 b a s e a l t u r a = 1 2 2 v t v t = v 2 t 2

Como o campo é uniforme, o fluxo é:

ϕ B = B A = 0,350 5,20 2 t 2 = 9,464 t 2

No instante t = 3,00   s , ϕ B = 9,464 3,00 2 = 85,2   W b .

Passo 2

De acordo com a lei de Faraday, a fem é dada por:

ε = d ϕ B d t = 9,464 d t 2 d t = 18,93 t

Quando t = 3,00   s ,

ε = 18,93 3,00 = 56,8   V

Passo 3

Se a força eletromotriz é ε = a t n , podemos descobrir quanto vale cada uma das incognitas apresentadas. Vamos igualar a expressão do passo anterior:

18,93 3,00 1 = a t n

Logo, a = 18,93 , t = 3,00 e n = 1 .

Resposta

  1. ϕ B = 85,2   W b ;
  2. ε = 56,8   V ;
  3. n = 1 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 30-44, uma semicircunferência de fio de raio a = 2,00c m gira com uma velocidade angular constante de 40 revoluções por segundo na presença de um campo magnético uniforme 20m T . Determine (a)
Uma espira retangular, com uma área de 0,15m 2 , está girando na presença de um campo magnético uniforme de módulo B = 0,20T . Quando o ângulo entre o campo e a normal ao plano da espira é π / 2 e est
Na Fig. 30-49, uma espira retangular de comprimento a = 2,2c m , largura b = 0,80c m e resistência R = 0,40m Ω é colocada nas vizinhanças de um fio infinitamente longo percorrido por uma corrente i =
Na Fig. 30-48, uma espira quadrada com 2,0c m de lado é submetida a um campo magnético, dirigido para fora do papel, cujo módulo é dado por B = 4,0 t 2 y , onde B está em teslas, t em segundos e y em
A Fig. mostra um bastão condutor de comprimento L sendo puxado ao longo de trilhos horizontais condutores, sem atrito, a uma velocidade constante v → . Um campo magnético uniforme vertical B → preench