Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.9 - Ex. 25
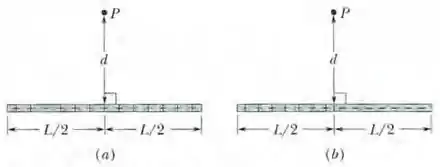
(a) A figura (a) mostra uma barra não condutora de comprimento e densidade linear de cargas positivas uniforme . Considere no infinito. Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
(b) A figura (b) mostra uma barra idêntica à do item (a), exceto pelo fato de que a metade da direita agora está carregada negativamente; o valor absoluto da densidade linear de cargas continua a ser em toda a barra. Com no infinito, qual é o valor de no ponto ?
Passo 1
Fala aí! Tudo certinho? 👀
Na primeira parte desse problema temos uma barra na horizontal de comprimento e densidade linear de cargas uniforme .
Na outra parte do problema temos a mesma barra, mas com metade da barra carregada positivamente e outra metade negativamente.
A partir daí queremos saber qual o valor do potencial em um ponto a uma distancia do centro da barra.
Tem ideia de como fazemos isso? 😬
Passo 2
Vou invocar uma fórmula meio grandinha aqui:
É o potencial produzido por uma barra carregada (falando bonito: uma distribuição linear retilínea de cargas), onde é o comprimento da barra, é a distância do ponto até a extremidade da barra e é a densidade linear de cargas. Esse ponto deve estar sobre a vertical que passa pela extremidade da barra.
Se eu fosse você eu não decoraria a fórmula e tentaria entender a dedução dela (que está nas páginas 86 e 87 dessa edição do Halliday), mas sei lá, vai que já é a véspera da prova (ou o dia kkkk). Você que decide.
Passo 3
Vamos substituir, mas cuidado! Na fórmula, o comprimento da barra é e, na questão, são duas barras de comprimento (unidas)! Então, vamos trocar, na fórmula, por e multiplicar tudo por :
Substituindo os valores do enunciado...
Tranquilo até aqui? 😉
Passo 4
Para o item b) é rápido! Você viu que na letra (a) a gente multiplicou por 2, já que eram duas barras iguais somadas (na verdade era uma só, mas cada uma das duas barras era a metade da original)? Viu? Ok. A gente multiplica por porque a contribuição de cada barra (ou cada metade) é igual. Se você inverte o sinal de uma metade, a contribuição continua igual, só que com o sinal oposto. Então quando você soma, dá zero!
Resposta rápida: Por simetria, é zero.
E aí! O que achou? Responde Aí! 😐
Resposta
Letra (a):
Letra (b): Por simetria, é zero.