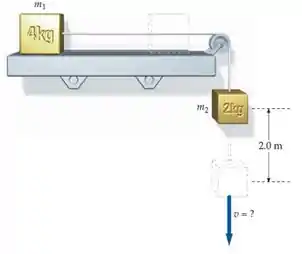
Na figura abaixo, o coeficiente de atrito cinético entre o bloco de e a prateleira é . (a) Encontre a energia dissipada por atrito quando o bloco de cai por uma distância . (b) Encontre a variação na energia mecânica do sistema dois-blocos-Terra durante o tempo que o bloco de leva para cair pela distância . (c) Use seu resultado da parte (b) para encontrar a rapidez de um dos blocos depois que o bloco de cai por .

(b) Nós queremos calcular a variação de energia mecânica no sistema inteiro (inclusive a Terra), então as trocas de energia mecânica não vão afetar nossa conta.

A única variação de energia mecânica acontece quando ela se dissipa em energia térmica, que é exatamente o que acabamos de calcular:

E então a variação de energia mecânica é:

(c) Vamos escrever uma equação para a energia total do sistema. A energia potencial gravitacional do bloco de vai se converter no seguinte: as energias cinéticas dos blocos e a energia térmica que inevitavelmente será dissipada.

E a velocidade dos dois blocos é a mesma:

Agora é só substituir os valores no caso em que o deslocamento do bloco pendurado é de :