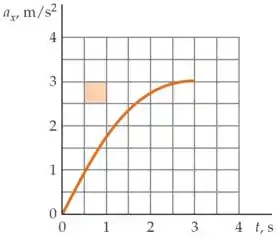
A figura abaixo mostra a aceleração de uma partícula em função do tempo. (a) Qual é a magnitude, em , da área da região sombreada? (b) A partícula parte do repouso em . Estime a velocidade em , e contando os quadrados abaixo da curva. (c) Esboce a curva vs. a partir dos seus resultados no item (b); depois estime o quanto a partícula viaja no intervalo de até .

(b) A área sob um gráfico da aceleração em função do tempo dá a velocidade da partícula, então para estimar a velocidade em cada um dos instantes de tempo pedidos, só precisamos contar os quadrados até aquele ponto.

Em , por exemplo, temos que estimar a seguinte área:

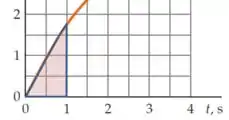
Nesse intervalo é razoável dizer que temos, mais ou menos, três quadrados e meio, e como cada quadrado equivale a :

E fazendo o mesmo para os outros intervalos (até e ), encontramos os outros valores:

(c) Se queremos esboçar um gráfico da velocidade usando apenas os pontos que acabamos de calcular, podemos começar fazendo uma tabela:

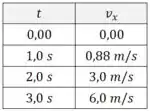
E agora desenhamos uma malha quadriculada e então simplesmente traçamos uma linha que passe pelos pontos. É importante desenhar a malha de forma que possamos usá-la para “contar os quadrados” para estimar a área:

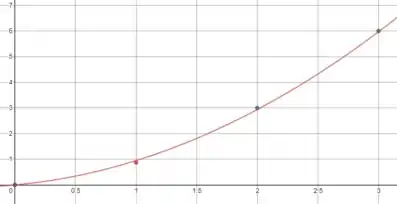
E agora podemos usar esse gráfico para estimar o deslocamento no intervalo : essa é apenas a área sob o gráfico nesse intervalo.

Cada um dos retângulos do nosso gráfico tem uma área que corresponde a , e temos aproximadamente quadrados no intervalo, então o deslocamento é: