Considere o gráfico da velocidade na figura abaixo. Assumindo x = 0 em t = 0 , escreva as expressões algébricas corretas para x ( t ) , v x ( t ) e a x ( t ) com os valores numéricos apropriados inseridos para todas as constantes.

A velocidade é v x t = - 10 m s 2 t + 50 m s , a aceleração é a x t = - 10m / s 2 e a posição é x t = - 5 m s 2 t 2 + 50 m s t .

Enunciado

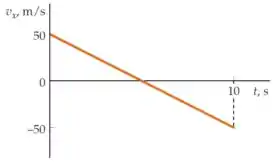
Vamos começar escrevendo a função da própria velocidade a partir do gráfico, porque a partir dela nós podemos determinar todas as outras.

O gráfico dado no enunciado é uma reta, então estamos procurando uma função do seguinte tipo:

é o coeficiente angular da reta, e pode ser calculado usando a fórmula que já conhecemos:

Onde é um intervalo qualquer no eixo vertical e é um intervalo correspondente qualquer no eixo horizontal:

E a constante é simplesmente o ponto onde a função cruza o eixo vertical:

E então ficamos com a seguinte função para a velocidade:

Agora vamos encontrar e a partir dessa função. Começamos com a aceleração, vamos lembrar da relação entre ela e a velocidade:

E agora vamos calcular a função da posição, que é simplesmente a integral de em relação ao tempo:

E como o enunciado diz que , a nossa função fica da seguinte forma:

A velocidade é , a aceleração é e a posição é .