Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.7 - Ex. 18

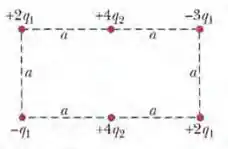
A figura abaixo mostra um arranjo retangular de partículas carregadas mantidas fixas no lugar, com a = 39,0 cm e as cargas indicadas como múltiplos inteiros de q1 = 3,40 pC e q2 = 6,00 pC. Com V = 0 no infinito, qual é o potencial elétrico no centro do retângulo? (Sugestão: examinando o problema com atenção, é possível reduzir consideravelmente os cálculos.)

Passo 1

Boom meus queridinhos, por aqui a gente não paraa !!

O que nós queremos saber aqui é o potencial elétrico no centro do retângulo, certo?

Vamos olhar mais de perto?

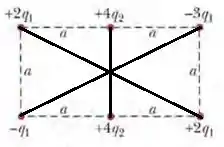
Boom, agora vamos lebrar como se calcula o potencial?

V = k . ∑ q i r i

Passo 2

As cargas dos cantos são equisdistantes ao ponto central, r , e as do centro, a 2 . Colocando na fórmula:

V = k 2 q 1 r + 4 q 2 a 2 - 3 q 1 r + 2 q 1 r + 4 q 2 a 2 - q 1 r

V = k 2 q 1 - 3 q 1 + 2 q 1 - q 1 r + 4 q 2 + 4 q 2 a 2

E olha que legaaal, quando nós reorganizamos estes ternos vemos que as cargas q 1 se cancelam e isso já vai facilitar nossa vida, porque não precisamos calcualr o r !!

Passo 3

Olhem só como fica depois de cancelarmos tudo:

V = k 16 q 2 a

Sabendo que:

k = 8,99 × 10 9 N m 2 C 2

q 2   =   6,00 × 10 - 12 C

a = 0,39   m

Substituindo:

V = 16 8,99 × 10 9 N m 2 C 2 6,00 × 10 - 12   C 0,39   m = 2,21   V

E é isso aí galerinha !! O que acharam ?!

Resposta

V = 2,21   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura abaixo, sete partículas carregadas são mantidas fixas no lugar para formar um quadrado com 4,0 cm de lado. Qual é o trabalho necessário para deslocar para o centro do quadrado uma partícula
Suponha que N elétrons possam ser colocados em duas configurações diferentes. Na configuração 1, todos os elétrons estão distribuídos uniformemente ao longo de um anel circular estreito de raio R. Na
A partir de Eq. 24-30, escreva uma expressão para o campo elétrico produzido por um dipolo em um ponto do eixo do dipolo.
Três partículas, de cargas q 1 = + 10 μ C , q 2 = - 20 μ C e q 3 = + 30 μ C , são posicionadas nos vértices de um triângulo isósceles, como mostra a Fig. 24-57. Se a = 10 c m e b = 6,0 c m , determine
As cargas e coordenadas de duas cargas pontuais situadas no plano xy são q 1 = + 3,00 × 10 - 6 C, x = + 3,50 cm, y = + 0,50 cm e q 2 = - 4,00 × 10 - 6 C, x = - 2,00 cm, y = + 1,50 cm. Qual é o trabalh