Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.2 - Ex. 28
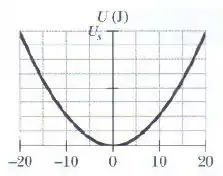
A figura mostra o poço de energia potencial unidimensional no qual se encontra uma partícula de [a função é da forma e a escala do eixo vertical é definida por ]. (a) Se a partícula passa pela posição de equilíbrio com uma velocidade de , a partícula retorna antes de chegar ao ponto ? (b) Caso a resposta seja afirmativa, calcule a posição do ponto de retorno; caso a reposta seja negativa, calcule a velocidade da partícula no ponto
.
Passo 1
Show de bolinhas galerinha, primeiro vamos começar lembrando do seguinte: a energia total do sistema é constante. No gráfico, a energia representada é a potencial, mas temos a cinética também. Elas seguem essa relação aqui:
Onde é a energia total. E pela lei de conservação de energia, podemos dizer o seguinte:
Belezoca, então bora lá ver como que fica essa brincadeira.
Passo 2
(a) Ok, agora vamos aplicar a lei de conservação.
Se a partícula passa pelo ponto de equilíbrio (onde a energia potencial é nula) com velocidade , a primeira parte da lei de conservação fica assim:
Ok, agora olhando o gráfico, pra chegar até o ponto , ele precisa ter energia potencial:
Ou seja, a lei de conservação ficaria assim:
Mas energia cinética negativa não existe! Ou seja, esse movimento é impossível, então a partícula retorna antes de chegar no ponto .
Passo 3
(b) Então, aonde é o ponto de retorno?
Já vimos que qualquer ponto vai ter que satisfazer essa relação aqui.
No ponto de retorno, a energia cinética vai ser exatamente zero, então:
E olhando o gráfico, isso é mais ou menos:
(Porque cada traço do eixo vertical “vale” , e então o ponto de eneria vai ser um pouco antes do terceiro traço.)
Passo 4
Outra forma de resolver isso é pegar algum ponto do gráfico pra achar o valor de naquela fórmula que o enunciado deu:
Logo:
E então aquela igualdade que usamos no início (para o ponto de retorno) ficaria:
Segue que:
O que bate com o resultado que tínhamos achado no “olhômetro”!
Resposta
(a) Sim, a partícula retorna.
(b) .